摘要

本文研究了分裂单极磁场中克尔黑洞(BH)周围磁彭罗斯过程(MPP)中的粒子动力学和加速度。磁化黑洞周围带电粒子运动的特征揭示了电离开普勒盘行为的四种不同可行模式:在规则的周转运动中存活;变为混沌环面态;由于沿磁力线逃逸而坍缩，由于落入黑洞而坍缩。利用有效势，我们研究了赤道内和赤道外平面稳定圆轨道的位置。我们观察到，正磁场\({{\mathcal {P}}}>0\)增加了有效电位的稳定性，而\({{\mathcal {P}}}<0\)降低了有效电位的稳定性。我们的研究表明，由MPP控制的旋转超大质量黑洞的超高效能量提取可以支付账单。我们预计中性粒子电离，如中子β衰变，会逐渐靠近黑洞视界，在质量为\(10^9M_{\odot}\)的超大质量黑洞中，质子的电荷超过\(10^{20}\)eV，磁场强度为\(10^4\)G。

1 介绍

活动星系核、伽马射线暴和x射线双星被认为是我们宇宙中最迷人、最强大的系统。据信，它们的能量来自一个主要机制，由一个磁化的、自旋的实体组成，就像黑洞或中子星[1]，或者来自一个环绕的吸积盘[2,3]。Blandford和Znajek[4]观察到黑洞周围的电磁场是无力的，因为它们与其他自由度解耦。因此，无力电动力学方程可表示为

（1)

式中、分别为规电位和电磁场强度，为电流。事实上，它们是经典的麦克斯韦方程，具有守恒的电磁能量-动量张量和不灭电流。Blandford-Znajek机制，也被称为磁化的Penrose机制，允许从旋转的黑洞中提取能量[5,6]。Blandford和Znajek开启了对上述机制的系统解释，以找到Kerr黑洞附近FFE方程1的微扰解。这种解的最简单形式被称为Blandford-Znajek单极子，它可以直接转换为在BHs附近具有磁源的分裂单极子解。对于Kerr BH, Blandford-Znajek单极子可以表示为自旋参数中的扰动，其中M和J分别表示质量和角动量[7]。而磁单极子在。

黑洞周围磁场的存在对吸积过程和带电物质都有重要影响。发现黑洞具有导电等离子体产生的吸积盘，其运动可以构成规则的磁场。最近的一项发现表明，银河系中心超大质量黑洞附近存在的强磁场与吸积盘无关[8]。因此，黑洞可以沉浸在黑洞视界附近具有复合结构的外磁场中，而其性质将是简单的，在更大的有限距离上与均匀磁场相邻[9]。Kovar等[10]观察到磁星赤道面的BH在距离较远的情况下可以浸入均匀磁场中。由Reissner-Nordström或Kerr-Newman时空概述的带电粒子动力学方程可以很容易地分离和集成[11]。粒子的这种动态运动已经在各种文章中进行了研究[12,13,14,15,16,17,18,19]。Konoplya[20]通过研究磁化黑洞周围的粒子动力学，推断潮汐电荷对有质量和无质量粒子的运动都有强烈的影响。而在[21,22,23,24,25,26,27,28,29,30]中可以找到磁化黑洞时空中带电粒子运动的丰富而详细的研究。在膜世界Kerr和Kerr - newman - kasuya BHs[31,32,33]中分别研究了遍力区域内的粒子碰撞和粒子运动。

弱磁场对中性粒子的动力学或背景几何结构的影响较小。然而，磁场对带电测试粒子的动力学有足够强的影响。结果，质量为m和q的带电测试粒子围绕一个质量为m的黑洞在强度为b的磁场中旋转，因此，我们可以建立一个无因次量，可以定义为相对洛伦兹力[34,35]。在磁场较弱的情况下，由于比电荷q/m的值较大，这个量也会有较大的值。在目前的工作中，我们认为“带电粒子”可以表示在吸积盘最内层旋转的任何种类的物质，从电子到一些带电的非均匀性[36]。

在本文中，我们的目的是研究旋转黑洞的磁层，之前研究的是一个分裂的单极解[4]。Komissarov[37]发现，对于来自黑洞附近薄吸积盘的原始磁场，或者来自黑洞视界附近另一个黑洞吸积分布的原始磁层，对分裂单极磁场的径向研究是可以接受的[38]。为了使我们的计算简单，我们将在本文中使用。

2 黑洞磁层

2.1 克尔黑洞

旋转Kerr黑洞在Boyer-Linquist坐标系()下的时空几何可以表示为

（2）

与

（3）

在哪里

（4）

在上述表达式中，M和a分别表示黑洞的质量和自旋参数。度规2，约化为史瓦西黑洞。度规2的视界可由

（5）

假设。上式中，和分别表示事件视界和柯西视界。对于最大旋转和非最大旋转，分别对应于Kerr BH的极值和次极值。在Boyer-Linquist坐标系中，时空度规2在点变得奇异，而视界的角速度可以表示为

（6）

2.2 将莫无极磁场

虽然引力是由优雅的克尔黑洞时空解(2)给出的，但黑洞视界前提下的外部磁场可能非常复杂。磁化环面结构的广义相对论磁流体动力学(GRMHD)模拟[39]显示环面结构中存在复杂且高度动态的磁场，但靠近结构旋转轴的外部磁场(射流可能在其中建立)与独立于原始磁场构型的分裂单极子或抛物磁场有关[40]。“大规模射流形成的抛物线解”[41]——靠近黑洞的磁单极子[5]，抛物线和磁单极子的磁场解非常相似。这种规则的抛物线磁场解与分裂的单极磁场解难以区分。

由于这些原因，利用单电荷测试粒子动力学来探索分裂单极子BH磁层模型，并在天体物理过程的几个重要研究中使用，是非常相关的。重要的是要注意，即使在这种情况下，这个因子仍然是非零的，这可能会导致足够大的黑洞和强磁场产生强大的加速过程。

一般来说，如果磁场包含非零极向元素，遍历层内的每个观察者都会感知到非零电场[42,43]。非零电场会导致带电粒子选择性吸积，从而产生感应电荷，为粒子加速提供静电能。如[44]所示，该电场不应被等离子体屏蔽[45]。如果满足以下条件，则可以屏蔽电场

（7）

同时满足，而和表示lnrf中记录的磁场和电场矢量。可以证明[44]，在遍历层之外是负的，而在遍历层内是正的。因此，由BH旋转和分裂单极磁场共同作用产生的感应电场在遍层内不经过筛选，可以作为有效的带电粒子加速器。

原则上，磁单极子在电磁学理论中是不存在的，因此在磁场的情况下，我们得到

（8）

分裂单极磁场的起源被认为是在赤道平面上的一个无限小薄的圆盘上绕着坐标系运动的电流。我们假设BH的磁层为分裂单极解[4]，可以借助电磁4向量势表示为

因此，它的非消失项可以描述为

这里B是磁场的强度。将分裂单极磁场视为与式(2)中给出的克尔BH度规具有相同的对称性。通过利用坐标变换，笛卡尔坐标为

（9）

目录

摘要 1 介绍 2 黑洞磁层 3.带电粒子动力学 4 磁彭罗斯过程中的粒子加速 5 天体物理相关性 6 有限公司 ncluding讲话 数据可用性 改变历史 参考文献 致谢 作者信息 搜索 导航 #####

3.带电粒子动力学

本节旨在探讨克尔黑洞周围带电粒子(质量为m，电荷为q)的运动特征，条件为。因此，通过分离变量技术，式(2)给出的度规的测地线运动可以用Hamilton-Jacobi方程表示为

（10）

式(10)中，和S分别表示hamilton和Jacobi作用。此外，是粒子的四动量。时空对称性允许我们用度规系数(3)定义相应的守恒能量和角动量为

(11) (12)

这里点表示对固有时求导。在带电粒子运动的情况下，比电荷和磁场可以定义为。因此，通过使用L，式(10)中的哈密顿量修改为

（13）

与

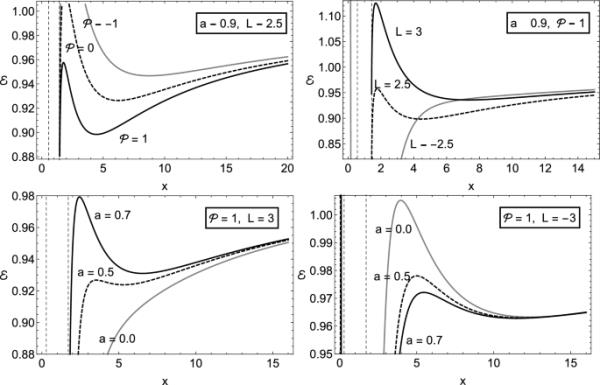
不同黑洞参数值下有效势的离赤道图形描述

（14）

在上面的表达式中，表示哈密顿函数的势部。利用方程。式(11)、(12)中，和的值可得为

(15) (16)

的约束所施加的能量边界可以限制带电测试粒子的运动。通过利用能量条件，有效势可以与比能相关，在克尔黑洞的情况下，其形式为[46]

（17）

在这里

除了赤道面上的粒子动力学外，黑洞周围磁场的存在会产生带电粒子动力学的混沌行为。在赤道平面上，有效势的极小值和极大值分别对应稳定和不稳定的圆轨道。克尔黑洞的圆轨道可以分为四种不同的类型，即带;逆行拉莫尔轨道(RLO)拉莫尔轨道(PLO):逆行反拉莫尔轨道(RALO)，详见[35]。其中，和分别表示共旋转粒子和反旋转粒子，而，分别定义排斥和吸引洛伦兹力。

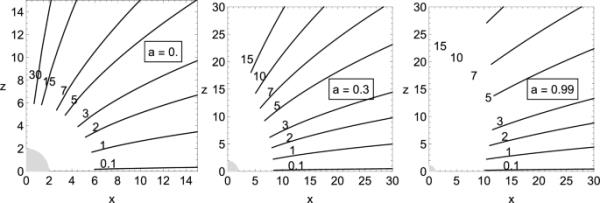
在不同的磁参数值下，离赤道稳定的圆形轨道的位置，而灰色的圆盘代表黑洞的外视界

带电粒子动力学可以用能量的边界来限定

（18）

为了更好地探索有效势(17)的性质，我们在图1中绘制了它在不同参数值下的行为。我们观察到，这增加了有效电位的稳定性，而降低了其稳定性。从无穷远处来的a和L值都较大的粒子，在a和L值较小的情况下，需要更多的能量在压缩中爬升，因此角动量L较小的粒子更有可能落入黑洞。角动量L负责两种类型的运动，即表示粒子的顺行运动，定义粒子的逆行运动。图1显示，顺行粒子比逆行粒子更接近黑洞，这与[47]的研究结果吻合得很好。带电粒子的存在及其在磁场中的动力学是磁场符号可能影响稳定性的潜在理由。带电粒子的行为可能会根据磁场是正的还是负的而变化，从而导致黑洞与其邻近物质之间的特殊相互作用。因此，这种相互作用可能会对黑洞系统的稳定性产生影响。

3.1 带电粒子轨迹

黑洞附近的圆轨道轨迹可以由开普勒吸积盘产生，而最内层稳定圆轨道(ISCO)决定了它的下边界。研究有效势的性质，可以得到粒子动力学的边界。因此，利用有效势的静止位置，可以得到带电测试粒子的圆形轨道

（19）

在Schwarzschild黑洞的情况下，有效势的局部极值仅位于赤道平面上，而在我们的情况下(Kerr黑洞)，非赤道平面上的局部极值也可以决定圆形轨道[48]。我们考虑并求解了离赤道平面有效势极小值的极端条件系统(19)。对于Kerr BH情况()，求离赤道面极小值位置的解析表达式有点困难，因此我们用数值方法计算了它。而对于的情况，离赤道稳定圆轨道的位置可以恢复为[36]

(20) (21)

在史瓦西黑洞的情况下，离赤道最内层稳定圆轨道位于，而在我们的情况下(和)，分别见图2。原则上，浸没在均匀外磁场中的黑洞附近带电粒子的运动具有混沌行为。尽管如此，在稳定的圆形轨道附近的带电粒子轨迹仍然具有结构化的性质[22]。观察到粒子在赤道面上也有结构轨迹，但随着倾角在赤道面上的变化，粒子的性质变得混沌。因为在我们的例子中，单极磁场与克尔时空几何的磁场具有相同的对称性，因此没有混沌轨迹。

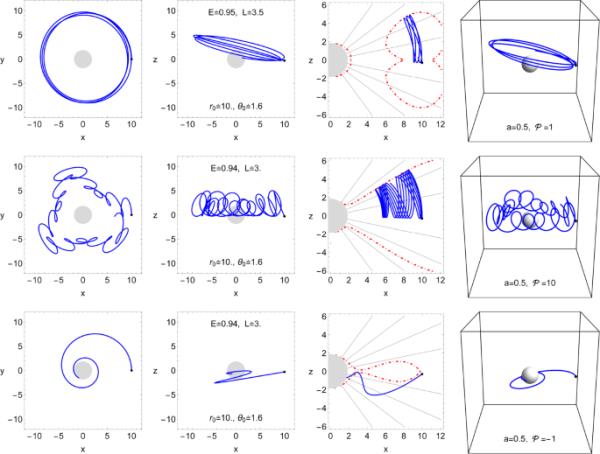
克尔黑洞(阴影圈)周围带电测试粒子轨迹(实线曲线)。第四列对应于三维粒子轨迹，而第一和第二列描述其二维部分。利用能量守恒和角动量守恒，我们可以在二维图(第三列)中描述四维位形空间(t, x, y, z)，其中运动的边界是通过有效势(虚点曲线)绘制的。

各种带电粒子，包括被分裂单极磁层的克尔黑洞捕获的带电粒子，详细描述见图3

带电粒子轨迹在分裂单极磁层中捕获并逃离克尔黑洞，详细描述见图3

有效势的特性可以引导我们找到各种能量边界。在克尔黑洞背景下，测试粒子轨迹的图形行为如图3赤道面所示，图4和图5为非赤道面所示。从图3的第一行和第二行可以观察到Schwarzschild和缓慢旋转的Kerr BH中带电粒子轨迹的差异。第三列的红色虚线对应着各种能量边界。第一种可能是指外部和内部边界的存在,测试粒子是被困在黑洞周围一些地区产生黑洞的视界外的环形形状(见图3和图4的第一和第二行),第二种情况代表的外边界BH抓住了带电粒子(见图4)的第三行。第三类对应的情况下内部和外部边界不存在,而黑洞可能捕获粒子，也可能逃逸到无限远。最后一种代表有内边界的情况，在这种情况下，粒子不是落入黑洞，而是逃逸到无穷远(见图5的最后一行)。

为了更好地理解磁性洛伦兹力和黑洞引力之间的相互作用，考虑磁性参数是必要的，这种相互作用通常会导致高度非线性和混沌的运动。我们注意到由于排斥洛伦兹力的响应而引起的规则运动和周转运动，从而导致粒子在圆形轨道上的稳定性。先前在均匀磁场[49]和抛物磁场[50]中发现了类似于排斥洛伦兹力的结论。但在辐射带电粒子的情况下，这种情况与均匀情况不同，因为其圆形停放轨道不稳定，粒子逐渐螺旋下降到黑洞[50]。

围绕史瓦西黑洞的中性测试粒子动力学被广泛认为是规则的和完全可积的。而带电粒子在磁性黑洞附近的运动通常是混沌的[51]。由于单极子的球对称性，带电粒子的运动仅在单极子分裂磁场排列时是规则的(可积的)[36]。在抛物线和均匀磁场的情况下，可以看到强烈的非线性和混沌轨迹。在我们的例子中，围绕圆形轨道的轨道即使有很小的周转振荡也是规则的[9]。这种近似圆形的轨迹在天体物理学中特别重要，因为它们调节着薄的(开普勒)吸积盘和环面流体结构。我们的发现表明混沌散射证实了单极子的球对称性。

4 磁彭罗斯过程中的粒子加速

中性吸积盘中粒子的电离可以通过许多不同的方式实现，例如原子电离或粒子衰变。另一个可行的假设是，吸积盘是一种准中性的带电粒子、离子(质子)和电子的混合物，它们围绕黑洞以圆形轨道运行。当圆盘中的物质足够厚时，带电粒子的主要自由路径相对于圆形轨道的长度非常短，并且带电粒子作为中性体一起运动。在圆盘的内边界附近，等离子体密度显著下降，带电粒子不再受到邻近粒子的抑制，开始自由运动，完全受到电磁场的影响。

本文提出的粒子电离模型在[52]中被引入，随后在[30,53,54,55]中也进行了研究，它自然地对应于磁性彭罗斯过程(MPP)[56,57]，即原始中性粒子分裂成两个带电粒子。这个简单的电离模型可以用来研究电离的开普勒盘的命运[54,58]，如果磁场影响较弱，它可以用来产生粒子在圆形轨道上的小振荡[59,60]。

粒子电荷和正则动量在电离过程中守恒[30]

（22）

可以证明，在电离时，动能是保留的

（23）

因为电磁贡献相互抵消[52,54]。在现实的情况下，产生的带电粒子中的一个可能比另一个质量大得多，例如，在原子电离的情况下，离子比电子质量大得多。质量逐渐增大的带电产物几乎吸收了其前身中性粒子的全部动能，而质量较轻的带电产物的动力学效应可以忽略不计

（24）

电离后，中性粒子将被分离成两个带电产物，在其总机械动量保持守恒的情况下，带电粒子将受到电磁场通过洛伦兹力的影响，其运动轨迹与中性粒子有很大的不同，如图6所示。

我们假设电离事件将发生在克尔黑洞赤道面附近，但有一些小的扰动使粒子也能在垂直方向上运动。中性母粒子将位于初始位置和四速度的球面轨道上

(25) (26)

粒子的运动常数由沿圆形轨道运行的电中性粒子的比能量和比角动量决定

(27) (28)

开普勒盘的内缘位于最内层稳定圆轨道(ISCO)上，其半径隐式由

（29）

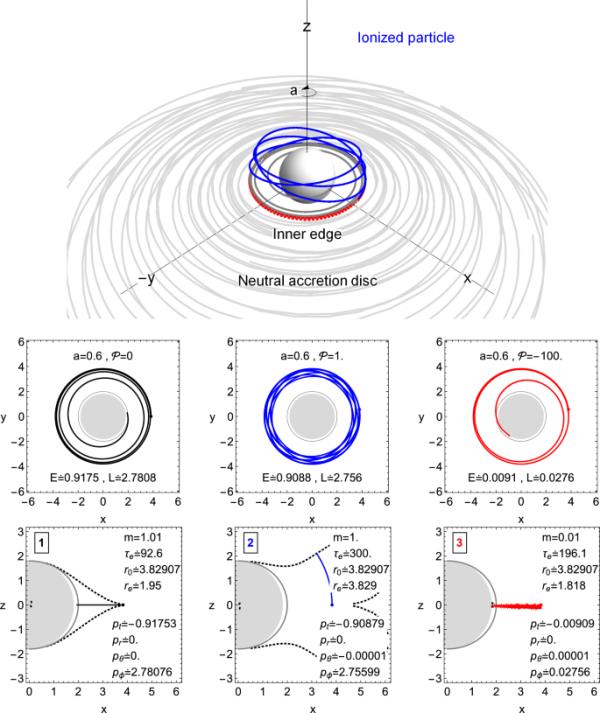
磁化旋转黑洞附近的粒子加速:第一个中性粒子(中子，黑色曲线)位于吸积盘的内缘，并开始落入黑洞，分解成两个带电粒子;第二个(质子，蓝色曲线)和第三个(电子，红色曲线)。第三个(红色)粒子带着大量的负能量落入黑洞，而第二个(蓝色)粒子带着过量的能量被困在黑洞周围的圆形轨道上

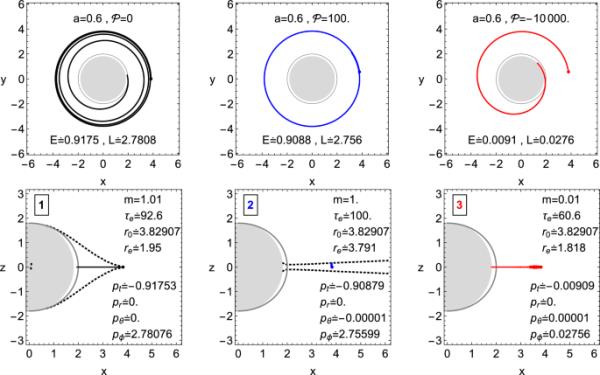
与图6相同的场景，但这次磁场参数值相对较小

MPP是一个区域机制，因此，它的能量平衡只能用电磁场的局域值来估计。中性粒子(中子)在薄的开普勒盘或厚的环面中围绕黑洞中心运行，处于束缚状态，其能量略小于1，这是为无限远处静止粒子保留的值。因此，第二个粒子(质子)的能量可以非常大，而第三个粒子的能量可以是负的，幅度非常大。由于引力场和磁场联合的混沌运动，第二个带电粒子的轨迹[52]和粒子的圆周运动将转变为沿着磁力线的直线运动，但在我们的情况下(在没有混沌运动的情况下)，第二个带电粒子由于其更高的能量而被困在黑洞周围的圆形轨道上。这种带电粒子流可以作为在许多活动星系核和类星体中观察到的相对论性喷流(或粒子风)的简单模型。第三个具有大负能量的粒子立即被黑洞捕获，如图6和7所示。

在不同的磁场参数离散值下，加速带电粒子的相同MPP过程如图6和7所示。可以清楚地观察到，在磁场较小的情况下，参数粒子轨迹的位置变化频繁(见图6)，而在磁场参数较大的情况下，被困粒子在圆形轨道上的位置更稳定(见图7)。

5 天体物理相关性

现实中的磁场太弱，无法影响背景时空

（30）

然而，就其对带电粒子运动的影响而言，它可能非常强大。施加在带电物质上的电磁洛伦兹力和引力的相互作用，用特定的电荷q/m来表示，可以用一个无量纲的“磁参数”来反映

（31）

式中P为分裂单极磁场大小，以高斯单位表示。带电测试粒子可以表示质子、电子、离子和大量带电差异，如带电尘埃或等离子体物体，其特定电荷q/m的范围从电子最大值到零。由于其特殊电荷q/m的量级相当大，在相对较弱的磁场下，质子、离子、主要是电子的磁场参数都可能是巨大的，因此在较弱的磁场下，电磁洛伦兹力对其动力学的影响是显著的。表1显示了一个包含质子和离子的比较分析。

如果MPP与电离的开普勒盘以及混沌色散过程相关联，则可以推断，在磁化旋转黑洞的情况下，由于捕获具有显著负能量的电子而提取黑洞的旋转能量，可能导致产生射流以极高的速度离开无穷大;因此，这是一个更复杂的Blandford-Znajek机制的基本过程[57]。

如果电离盘围绕非自旋黑洞(或被弱磁场包围的缓慢自旋黑洞)旋转，则MPP机制产生的风不会逃逸到无限远，其能量来自旋转物质的旋转能量(这象征着佩恩-布兰福德过程[61])。先前在开普勒盘内旋转的物质的旋转能量的转化导致了混沌散射过程引起的射流的产生，然而，与与电磁场加速度相关的能量相比，与圆周运动能量转化为平动能量相关的能量要小得多。

5.1 极端状态下MPP产物的超高能宇宙射线

宇宙射线与粒子能量的大量膨胀相一致。它们通常由高能离子或质子组成;注意到的各向同性色散表明它是银河系外的起源，对它们形成的解释一直存在争议。与能量为eV的粒子对应的超高能宇宙射线(uhecr)的观测——偶尔发现能量为eV的粒子，由于与宇宙微波背景的相互作用而超过了eV的GZK极限——特别有趣[30]。对能量大于GZK极限的粒子的研究意味着对这种高能粒子的源有严格的距离限制。

能量为eV的粒子的极端加速度很难解释。尽管如此，我们还是可以提出一种直接的方法，如果MPP在一个被足够强的磁场包围的超大质量黑洞附近活动，那么它就会以超高效率的状态为中心。在极有效的情况下，由MPP产生的带电粒子的能量可以表示为

（32)

上式中，q和m分别为被测粒子的电荷和质量，e和分别为质子的电荷和质量。即使在具有质量的超大质量黑洞被微弱旋转的磁场包围时，也可能产生能量为eV的质子。

值得一提的是，可以得到超大质量黑洞SgrA的光子能量，在星系中心看到的相关磁场由

（33）

非常吸引人的是，这个量对应于所收集数据中众所周知的能量范围的拐点，即eV，在这里发现的粒子通量总量大大减少，这表明存在一个位于较近距离的极其强大的唯一源。在SgrA上实施的MPP建议将模型链接到eV的UHECR数据膝关节。

6 有限公司ncluding讲话

由于GRMHD模拟表明，黑洞周围的实际磁场可能具有相对复杂的性质[37,38]。在目前的工作中，我们利用分裂单极磁场作为具有径向性质的大尺度黑洞磁层的基本模型。

利用有效势，我们研究了赤道内和赤道外平面稳定圆轨道的位置。在考虑带电粒子运动轨迹的情况下，我们对运动方程进行了数值求解，并用图形演示了其在不同参数值作用下的行为。此外，我们观察到有效电位的稳定性增加，而稳定性降低。从无穷远处进入的a和L值较大的粒子比a和L值较小的粒子需要更多的能量来爬升，因此角动量L较小的粒子更有可能落入BH。图1显示，顺行粒子()比逆行粒子()的运动更接近黑洞，这与[47]的研究结果很吻合。

观察到带电粒子在赤道面上也有结构轨迹，而在非赤道面上，随着倾角随赤道面的变化，带电粒子的性质变得混沌。原则上，围绕磁化黑洞的带电粒子动力学揭示了电离开普勒盘行为的四种不同可行模式:(i)在规则的本轮运动中生存，(ii)转变为混沌的环形状态，(iii)由于沿着磁力线逃逸而坍塌(导致产生风和/或最有可能的射流，它们可能提供物质在垂直方向上逃离黑洞环境)以及(iv)由于落入黑洞而导致吸积物质坍塌。高频准周期振荡的发现可归因于由极弱磁场驱动的周转运动区域。在这种情况下，外部(电)磁场和黑洞旋转的引力效应的联合作用可能在某些条件下产生稳定轨道的区域。磁场可能对粒子有限制作用，这有助于它们有规律地运动。当磁场被扭曲或扭曲时，它们会导致混乱的活动，破坏粒子轨迹中的任何规则模式。这可能是由于弯曲时空几何中的磁场结构的复杂性，(局部)非轴对称结构或环境干扰而发生的。在第三种情况下，高能带电粒子可能由于MPP而逃逸。由于在我们的例子中，分裂单极磁场与旋转Kerr BH时空具有相同的对称性，因此可能没有像[55]那样的混沌(规则)轨迹，详见图3、图4和图5。这些状态的特征目前正在研究中，可能会根据黑洞及其吸积盘的参数而变化。

我们提出了一种超大质量黑洞产生超高能量宇宙射线的方法。利用一种独特的、超高效的MPP和中性粒子的电离机制，包括在旋转黑洞视界上衰变的中子。来自电离的开普勒盘的带电粒子可以在克尔黑洞附近加速，MPP效率超过，允许质子加速为能量。

在质量和G的超大质量黑洞附近的eV;在M87附近的eV，一个质量和G的超大质量黑洞;以及在SgrA附近的eV, SgrA是一个质量和G的超大质量黑洞。

以下是该模型的主要优点:

• 超大质量黑洞被预测为最高能量宇宙射线的来源

• 在可行的天体物理设置下，在其附近的超大质量黑洞中，具有适度的自旋和通常的磁场强度

• 并不依赖于粒子获得超高能量的扩展加速区，也不需要对吸积物质参数进行微调(详见[55])。

此外，通过研究旋转黑洞周围的能量提取过程，可以了解强引力和粒子相互作用和行为的影响。框架拖拽、引力时间膨胀和时空曲率对粒子轨迹的影响都是这种现象的例子。

原则上，所提出的方法可用于由巨大磁场补偿的小质量中子星。然而，这种类型的调查将留给未来的研究。因为相对论电子失去同步辐射的速度比质子快几倍，所以uhecr中较重的元素更有可能出现在这种情况下。

在建议的框架内预测候选的超大质量黑洞需要事件视界尺度的磁场数据。目前很少有这样精确的测量，但即将到来的全球VLBI观测应该会增加这个数字。我们认为提出的超大质量黑洞作为UHECR动力引擎的模型为理解这种独特的高能现象及其在各种高能环境中的适用性开辟了新的可能性。

下载原文档：https://link.springer.com/content/pdf/10.1140/epjcs10052-023-11897-x.pdf