摘要

本文在空间平坦的friedman - lema \({\hat{i}}}\)三- robertson - walker (FLRW)几何背景下，研究了标量张量引力理论中的复标量场。在标量-张量理论中，将标量场作为非最小耦合复场，利用诺特对称分析确定了标量场的经典宇宙学解。诺特对称分析不仅用于寻找对称向量和势，而且还有助于在增广空间中找到适当的变换\((a，~\phi，~\theta)\右行(u，~v，~\theta)\)，从而使其中一个新变量成为循环变量。在量子宇宙学中，我们在超小空间中建立了惠勒-德维特(WD)方程，并利用守恒(诺特)电荷的算符版本计算了它的解，即宇宙的波函数。最后，从观测的角度讨论了经典解的性质，并对宇宙奇点进行了经典和量子力学的检验。

1 介绍

自上世纪末以来，标准宇宙学面临着巨大的挑战，如何解释观测证据表明我们的宇宙正在经历一个加速阶段。为了在宇宙学的背景下适应这一事实，宇宙学家们分享了标准宇宙学的两种可能的修改。其中一个小组在爱因斯坦-希尔伯特作用[1]中引入了一个额外的术语(即引力理论的修正)，而另一个小组更喜欢爱因斯坦引力框架内的外来物质。这种奇异的物质被称为具有巨大负压的暗能量。一个假设的标量场(称为暴胀[2,3,4,5])负责早期加速进化时代，即暴胀时代。类似地，描述晚时间加速的标量场(称为暗能量[6,7,8,9,10,11,12])必须具有很大的- ve压力。

多标量场宇宙学在研究混合暴胀、双重暴胀、吸引子等方面具有重要作用。Quintom模型[13]和Chiral模型是两个众所周知的多标量场宇宙学模型。quintom模型(其中一个是quintessence场，另一个是phantom场)是DE模型，而Chiral模型导致双曲膨胀[14]。为了引入多标量场模型，可以考虑复标量场[15,16,17,18,19,20,21,22]的存在性，其实部和虚部等价于双标量场理论[23,24]。本文研究了复标量场的标量张量理论[25]。标量张量理论中的标量场与引力耦合最小，它与爱因斯坦广义相对论中的引力作用积分相互作用。标量张量理论通常用马赫原理[27]在Jordan坐标系中定义[26]。具有远平行引力的标量张量理论描述了标量扭转理论。

自上个世纪以来，对称性分析在量子场论研究时空的内部对称性、全局连续对称性和排列对称性方面发挥了重要作用[28,29]。特别是，诺特对称在识别与物理系统相关的守恒量方面起着重要作用。另外，Noether积分可以在很大程度上简化微分方程组[30,31,32,33,34,35]。此外，利用诺特对称，可以唯一地求出与物理系统的作用积分相关联的任意函数。

本文给出了用诺特对称分析方法求解具有复标量场的标量张量理论的宇宙学模型的一个例子。利用诺特对称分析得到了该模型的经典宇宙学解。与此系统相关的守恒量也得到了。在量子宇宙学的背景下，通过确定守恒电荷的量子版本解的周期部分，形成Wheeler DeWitt (WD)方程，得到宇宙的波函数。本文的计划如下:第2节给出了标量-张量宇宙学模型的基本方程，第3节用诺特对称方法求出了模型的解析解。在第4节中，我们讨论了目前宇宙学模型中WD方程的形成及其使用Noether对称方法的可能解，并在第5节中进行了简要的回顾。

在诺特定理中，变分的泛函的不变性或在力学中，作用积分的不变性是在无穷小变换下检验的。一般来说，这种变换是由一个称为诺特对称向量的微分算子产生的。然而，在目前的工作中，我们只局限于点变换。完整的分类可参考[36]。

2 标量张量宇宙学的基本方程

本文考虑了标量张量和标量扭转理论，其中标量场本质上是复杂的，并且与重力的耦合最小。考虑标量张量理论中的复标量场，作用积分的形式为[37]

（1）

这里R是通常的里奇标量它与度规张量的列维-奇维塔联系有关。也是复标量场，决定了它的范数，即。表示引力与标量场之间的耦合函数和驱动动力学的势函数。

如果耦合函数取的值为常数，则可以得到复标量场的Brans-Dicke理论，作用积分(1)变换为[37]

（2）

空间平坦的FLRW宇宙的线素可以写成

（3）

其中a(t)为比例因子，N(t)为延时函数。

里奇标量也取表达式为

（4）

H表示通常的哈勃参数，上面的点表示对宇宙时间t的微分。

利用里奇标量表达式(来自于式(4))对式(1)进行分部积分，得到类点拉格朗日量为

（5）

同样，对式(4)分段积分，得到Brans-Dicke理论的类点拉格朗日方程为

（6）

利用极坐标形式，复标量场可以写成

（7）

利用Eq.(7)，拉格朗日(6)变换为[37]

（8）

显然，上面的拉格朗日表示了一个多标量场宇宙学模型，其中是Brans-Dicke场，第二个标量场与重力最小耦合，也与重力最小耦合。此外，目前的宇宙学模型代表了FLRW模型中常见的Brans-Dicke场，具有一个宇宙学常数和一个不耦合的标量场，这种宇宙学模型在文献中得到了广泛的应用[38,39]。

对应于拉格朗日量(8)的Brans Dicke宇宙学模型的场方程可以写成

(9) (10) (11) (12)

3.用诺特对称方法解析解

如果一个物理系统的拉格朗日相对于李氏导数[40]沿一个适当的向量场保持不变，则相应的物理系统与一些守恒量相关联(Noether 's first theorem[41])。

如果是类点正则拉格朗日，那么，

（13）

为对应的欧拉-拉格朗日方程。

将(13)式与(一些未知函数)缩并后，得到如下结果

（14）

因此，拉格朗日的李氏导数为

（15）

这个由[42,43]定义的向量场

（16）

被称为对称的无穷小发生器。现在，根据诺特第一定理如果物理系统对于向量场是不变的。

诺特对称方法对于确定物理系统的守恒量非常有用。对称条件与沿无限小发生器具有守恒相通量的拉格朗日量的运动常数有关。此外，从式(15)中可以得出结论，与这个对称准则相关联的是系统的运动常数，称为诺特电流或守恒电流。定义为[30,44,45]

（17）

也满足条件

（18）

与该系统相关的能量函数可以写成[33,46]

（19）

如果拉格朗日函数没有明确地包含时间，那么这个能量函数，也就是系统的哈密顿函数，就是一个运动常数。利用这些对称约束，物理系统的演化方程可以求解或在很大程度上简化。

对于本模型，构型空间是一个三维空间。同样从拉格朗日公式(8)中，我们可以看到它是一个循环变量无穷小发生器的形式是

（20）

这里，，和是无穷小发生器和的系数

（21）

现在，把诺特第一定理应用到拉格朗日定理中

（22）

(22)式的显式给出了如下的偏微分方程组:

(24) (25) (26) (27)

对于上述偏微分方程组，可以采用分离变量法，即、、和。

解方程。一个人可以得到

（28）

式中，和是与关系的积分常数。

将式(28)和式(27)的值代入式(27)得到积分

（29）

其中，积分常数严格为正。

这样，在拉格朗日量上施加对称条件，就可以找到诺特对称的无限小产生源。此外，势函数是用对称准则确定的，而不是用现象学方法确定的。

诺特对称的另一个重要特征是与它相关的一些守恒量。对于弯曲空间中的场论来说，没有一个明确定义的能量概念。但是当系统中存在一个时间型杀伤向量时，就存在一个相关的守恒能量。众所周知，在FLRW时空中没有像时间一样的杀死向量。但拉格朗日密度与时间无关。因此，对于类点拉格朗日，我们可以定义一个守恒能量。因此，与此对称准则相关联的守恒量有两个，即守恒电荷(定义于式(17))和守恒能量(定义于式(19))，其显式如下:

(30) (31)

通常Eq.(17)给出与此对称准则相关的守恒电流。对守恒电流的时间分量在空间体积上积分，可以得到守恒电荷。但目前模型中的所有变量都是时间相关的。方程(30)给出了与这种对称相关的守恒电荷。此外，这个守恒电荷也可以表示为具有Cartan 1形式的无穷小发生器的内积[47]。

（32)

其中一种形式的定义是

（33）

表示与向量场的内积。

现在，我们要做一个点变换使u变为循环变量因为循环变量对于求解非线性耦合演化方程非常有用。对于上述变换，变换后的无穷小发生器的形式为

(34)

为了使u循环，可以将变换限制为

(35)

式(35)的显式形式为

（36）

式(36)实际上描述了旧坐标与新坐标之间的关系。然后使用Eq.(36)，将拉格朗日(8)变换为

（37）

这里A B C是任意常数。

变换后的拉格朗日的欧拉-拉格朗日方程可以写成

（38）

求解这组方程(38)可以把新变量写成

(39) (40) (41)

这里是任意常数。我们也可以用关系式(38)得到。我们可以根据这个值的结果来确定延时函数。

利用式(36)和式(39)~式(41)的解，可以求得旧变量下Brans-Dicke宇宙学模型演化方程的解为:

(42) (43) (44)

图1给出了无量纲尺度因子相对于无量纲宇宙时间的变化(这里是尺度因子的值，是哈勃参数在当前宇宙时间的值)。同样，无因次哈勃参数和减速参数q(t)也用图2和图3中无因次尺度因子的变化用图形表示。图1显示，在目前的模型中，宇宙是一个膨胀模型，膨胀速率逐渐减小，如图2所示。减速参数的图形表示表明，最初宇宙处于加速阶段，随后出现减速时代，然后目前宇宙又进入加速时代(图3)。最后需要提到的是，为了正确选择参数符号，模型的减速参数的当前值与观测值[48]。

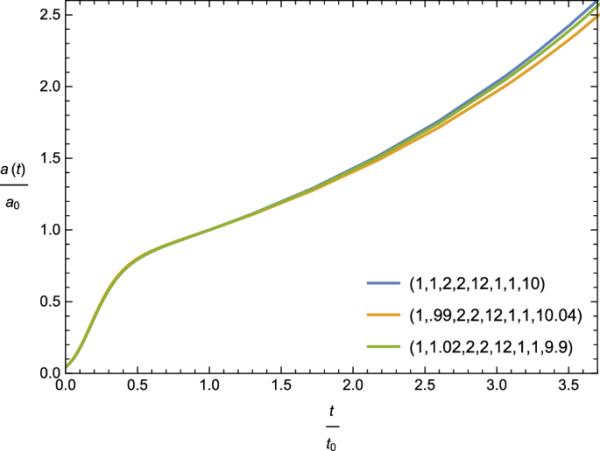
不同参数空间值的尺度因子相对于宇宙时间t的图形表示

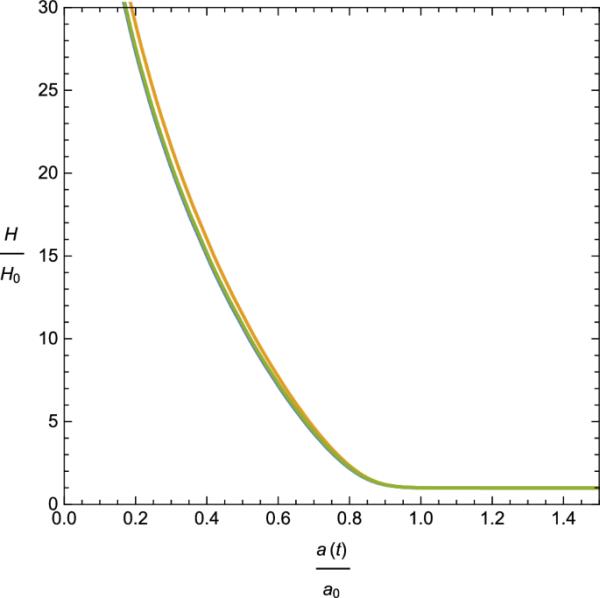
无量纲哈勃参数关于比例因子a(t)的图形表示

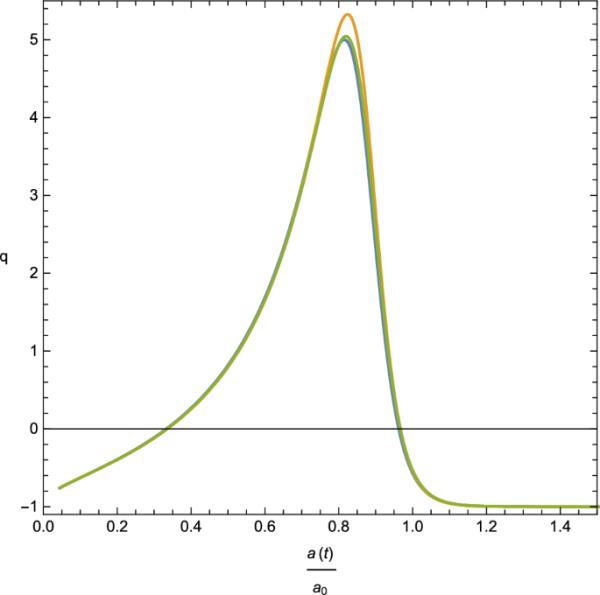
减速参数q(t)随比例因子a(t)的图形表示

4 宇宙的WD方程和波函数的形成:a des量子宇宙学的描述

在量子宇宙学的背景下，诺特对称条件可以改写为

(45)

这里H是系统的哈密顿量它对于推导Wheeler Dewitt (WD)方程非常有用，定义为

(46)

相空间中的对称向量。

在量子宇宙学的超空间模型中，对称分析可以恰当地解释宇宙的波函数如下:

守恒的正则共轭动量可以写成

(47)

其中m是对称的数目。

式(47)的运算符版本可以写成

(48)

上述式(48)给出了振荡解，由式给出

(49)

这里k代表没有对称的方向。因此波函数的振荡部分表明了诺特对称的存在。

在三维位形空间中，与该模型相关的标准共轭动量可以写成

(50) (51) (52)

那么这个系统的哈密顿函数是这样的

(53)

这里是任意常数。在量子宇宙学中，宇宙的波函数是惠勒-德维特(WD)方程的解。WD方程是一个二阶双曲型偏微分方程。实际上它是哈密顿约束的算子形式。WD方程可以写成，其中是哈密顿量的算符版本，是宇宙的波函数。但在转换为运算符版本的过程中，我们遇到了一个问题，称为运算符排序问题。这里，还有。则对应哈密顿量(53)的WD方程为

(54)

通过分离WD算子的特征函数，可以得到该方程的解:[49]

(55)

这里作为WD算子的本征函数，Q为守恒电荷，W(Q)为权函数。但是，由于极小超空间变量在WD算子中是高度耦合的，我们无法通过分离变量得到上述WD方程(54)的显式解。因此，可以使用新的变量来分析这个模型。因此，与类点拉格朗日量(37)相关联，标准共轭动量可以写成[50]

(56) (57) (58)

由于u和在拉格朗日量(37)中是循环的，在自然界中是守恒的。

则系统的哈密顿量为:

(59)

这里，，和都是任意常数。

如前所述，量化方案中的因子排序问题只不过是变量及其共轭动量的排序。因此，通过通常的算子转换，我们得到了六个参数的惠勒-德威特(WD)方程族

由于三重态和重态的选择有无限种可能，因此有无限种可能的排序。在文献中，对上述三连音和二连音有以下几种优选:

1. (i)

   维伦金算子排序:

2. (2)

   达朗贝尔算子排序:

3. (3)

   没有订购:

虽然波函数的性质取决于算子排序的选择，但半经典描述保持不变[50,51]。为了简单起见，我们将把自己限制在上面的第三种选择(即，无排序)，并且WD方程采用这种形式

(60)

求解Eq.(60)时，可以采用分离变量的方法

(61)

(56)和(58)的运算符版本可以写成

(62) (63)

用式(61)求解式(62)和式(63)可以得到

(64) (65)

和是积分常数。实际上方程式。(64)和(65)描述了波函数的振荡部分。

将和的值代入WD方程(60)，得到二阶微分方程为

(66)

式(66)的解描述了波函数的非振荡部分，由式给出

(67)

其中，I为第一类修正贝塞尔函数，函数表示为。，都是任意常数。所以宇宙的波函数变成

(68)

值得注意的是，给出了小超空间上的概率测度。

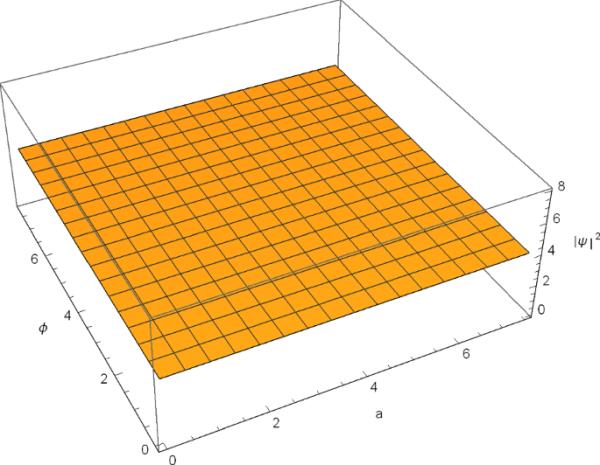
图4和图5表明，概率的度量取决于常数的符号。当或为整数时，在零体积处存在有限的非零概率，而在零体积处的概率为零。的负非整数值则不能定义概率。因此，量子描述允许大爆炸奇点，而量子公式克服了或整数的初始奇点。

对于半经典极限下的WKB近似，可以这样写

(69)

经典的HJ函数S可以展开成幂级数

(70)

因此，波包

(71)

用任意参数(即分离常数)表征经典解。以上WD方程的半经典极限给出了的HJ方程(零阶)

(72)

对于下面的显式解，分离形式是合适的

(73)

与

(74) (75)

和

(76)

这是分离常数和这是积分常数。

因此，波包(71)具有显式形式为

(77)

二元高斯分布在哪里，如果有，波函数将快速振荡，因此有可能提供相消干涉

(78)

这得到了经典解的支持。因此，通常，经典极限将在

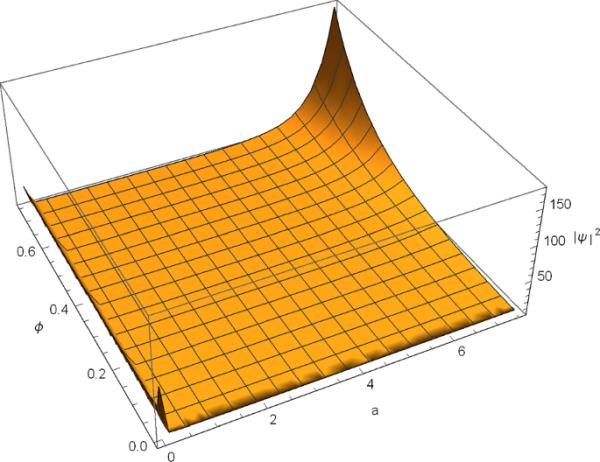
时间的图形表示

时间的图形表示

在爱因斯坦引力的度量公式中，有四个约束，其中超动量约束(一组三个)或矢量约束在本质上是齐次的小超空间中相同地消失。在量子版本中，唯一具有算子形式的非平凡约束方程就是WD方程，即哈密顿约束或标量约束

(79)

齐次自由度和可以从三个度规和共轭动量中推导出来现在类似于WKB近似如果波函数可以写成

(80)

那么从WD方程可以得到量子修正的Hamilton-Jacobi方程为

(81)

给定超空间的约化超度量在哪里[52]，类空间超曲面的标量曲率密度的特殊化是什么

(82)

被称为量子势。

现在，由于量子宇宙学中的因果解释，轨迹应该是真实的，独立于任何观测。这样的轨迹由相应的HJ方程确定。通过识别

(83)

用通常的动量-速度关系

(84)

一阶轨迹也就是

(85）

称为波西米亚轨迹(即量子轨迹)。可以注意到，这些量子轨迹在时间再参数化下是不变的[52]。

在目前的背景下，波西米亚轨迹的特点是(选择)

(86)

量子修正后的HJ方程是这样的

(87)

与

(88)

作为量子势的显式形式。

目录

摘要 1 介绍 2 标量张量宇宙学的基本方程 3.用诺特对称方法解析解 4 宇宙的WD方程和波函数的形成:a des 量子宇宙学的描述 5 简要总结 数据可用性 参考文献 致谢 作者信息 搜索 导航 #####

5 简要总结

本文研究了一个多标量场宇宙学模型，其中一个标量场与引力和另一个标量场都是非最小耦合的，而另一个标量场与引力是最小耦合的。由于高度耦合和非线性的场方程，目前的模型不能用通常的方法进行宇宙学研究。然而，这里展示了对称分析特别是诺特对称如何帮助我们从经典和量子力学角度分析当前的宇宙学模型。通过对称向量来识别循环变量，极大地简化了拉格朗日方程，从而使场方程可解。根据经典解，相关的宇宙学参数绘制在图1、2和3中。最具体地说，图1显示了宇宙在整个演化过程中不断膨胀。图2中无量纲的哈勃参数曲线图表明，宇宙虽然在膨胀，但膨胀的速度随着演化而逐渐减小。图3表明，目前的模型描述了大爆炸后进化的所有三个阶段(最初是加速阶段，随后是减速阶段，最后是现在的加速膨胀阶段)。通过对所涉及参数的合理选择，本文所提出的减速参数理论预测值与实测值相吻合。因此，有人可能会说，目前的模型至少在质量上与观测相符。诺特对称在用正则量子化分析量子宇宙学中起着至关重要的作用。量子宇宙学中的基本方程即WD方程是二阶双曲型p.d.e。守恒电荷的算子版不仅识别了波函数的周期部分，而且有助于求解WD方程。因此，人们可以研究大爆炸奇点是否可以通过量子描述消除。结果表明，只要选择适当的参数，就可以用量子公式避免奇异性。因此，诺特对称分析对于研究任何宇宙学模型都起着至关重要的作用。

下载原文档：https://link.springer.com/content/pdf/10.1140/epjcs10052-023-11875-3.pdf