摘要
尽管地质建模技术取得了重大进展,但准确估计水力裂缝半长仍然是一项具有挑战性的任务。本文介绍了一种较为新颖的高斯压力瞬态(GPT)估计方法。GPT方法是迭代的,确保了快速收敛,并根据高斯衰减曲线分析(DCA)获得的预定水力扩散系数值提供了水力裂缝半长b的可靠估计。为了验证GPT的结果,研究人员将位于德克萨斯州西部Midland盆地Wolfcamp页岩地层的两口井的生产数据与传统的速率瞬态分析(RTA)方法结合使用。此外,GPT方法提供了概率估计水力裂缝半长的能力,提供了两种创新的方法来评估这种新开发的方法在确定性和概率估计方面的鲁棒性。模拟结果表明,高斯方法与微地震裂缝半长有密切的相关性,与经典的rta方法有单独的证实。通过本文的案例研究,gpt方法在估算Wolfcamp的两口案例井的水力裂缝半长方面展示了它的实用性,有效地证明了这种新方法的有效性和实用性。
介绍
水力压裂已经成为一种广泛应用的增产技术,用于提高低渗透油藏的油气产量(Montgomery & Smith 2010)。通过对井筒周围区域进行压裂,可以建立一个更高渗透率的区域,更重要的是,可以增加储层与井系统之间的接触面积,从而增加与储层的接触。近二十年来,水力压裂技术在非常规油气资源开发中得到了广泛应用(Ostojic et al. 2012;Tiab & Donaldson 2015),具有极低渗透率、低孔隙度和高非均质性的特点(Khan & Al-Nakhli 2012)。除非采用水力压裂增产,否则这种非常规油藏的生产是不经济的(Medavarapu et al. 2017;Taha et al. 2013)。
水力压裂处理包括注入流体以施加水力增强压力,从而打开井眼射孔处的新裂缝。在压裂液中加入支撑剂,以在新形成的裂缝中保持一定的剩余孔径。支撑剂将有助于保持井筒周围裂缝区域的张开,并提高油气采收率(Khan & Al-Nakhli 2012)。至关重要的是,水力压裂井系统的油气产量将主要取决于工程干预产生的裂缝长度和裂缝高度,因为所有其他储层性质都是由大自然预先决定的。
在我们的研究中,假设有效裂缝半长由具有无限导流性的裂缝段组成,这些裂缝段可以有效地将储层流体通过井筒输送到地面进行采收。在压裂工艺设计中,考虑最佳裂缝半长,因为裂缝半长越长,采收率越大(Guo 2007;Muther et al. 2020)。然而,压裂处理后的井况分析经常表明,有效裂缝半长往往小于设计或模拟长度(Barree et al. 2005;Cipolla et al. 2008)。实际裂缝半长与计划裂缝半长之间的差异似乎是由两个能力差距造成的:1)在每个射孔簇的压裂和将支撑剂输送到地层中以保持较长有效半长裂缝的工程成功方面仍然有限(Nandlal & Weijermars 2022a, b;(2)具有可靠预测能力的裂缝建模仍然缺乏(Tugan & Weijermars 2022a, b)。裂缝半长模型估计与实际裂缝之间的差距通常归因于“复杂的裂缝几何形状”(Elbel & Ayoub 1992)。
对压裂后裂缝半长进行可靠的估计,是进入学习曲线、改进未来页岩压裂处理的基础。速率-暂态分析(RTA)和压力-暂态分析(PTA)模型是估计有效裂缝半长的经典方法(Cipolla & Mayerhofer 1998;Bahrami et al. 2015)。然而,当渗透率已经得到很好的约束时,这些方法是最准确的。对于非常规资源,需要很长时间才能积累压力来估计渗透率,这使得结果具有很大的不确定性。其他工具,如生产数据分析(PDA),可以在不关井的情况下计算裂缝半长(Rushing & Blasingame 2003)。然而,PDA的一个缺点是它受生产数据质量的高度影响,这可能再次导致估计具有很高的不确定性。微地震制图是一种实用的现场工具,可以提供图像来估计水力裂缝的几何形状(Gutierrez等,2010)。这种测绘工具的一个局限性是,它给出的是最大裂缝半长,而不是对油气产量有贡献的有效半长(Ibrahim et al. 2020)。
目前的研究评估了扩散系数方程的基于物理的高斯解(Weijermars 2021, 2022a)是否可以应用于提供可靠的裂缝半长估计。基于压力扩散方程的新解,提出了高斯衰减曲线分析(DCA)、高斯压力瞬态模型(PTA)和高斯油藏模型(Weijermars 2022a)三种应用模式。对于高斯PTA模型,要估计裂缝半长,首先要获得可靠的水力扩散系数值(Weijermars & Afagwu 2022)。高斯DCA方法可通过以下高斯DCA方程(Weijermars 2022a, b)对历史生产数据进行历史匹配,得到所需的水力扩散系数:
(1)式(1)可用日产量数据应用。对于油井,初始井速(生产的第一天)设定为1桶/天;对于气井,建议使用1毫立方英尺/天(Weijermars 2022a)。该术语是无量纲的,但其参数的规范化是使用单位度量来实现的,例如将t替换为无量纲单位(例如,t = 1代替tdimensional = 1天,或10代替10天,等等)并使用无量纲Dh(例如,Dh = 1等于一个量纲输入Dh_dimensional为1 ft2/day)。
目前研究的主要新颖之处在于从油井生产数据中估计裂缝半长,这传统上需要专业知识和RTA的应用。与传统方法相比,新提出的高斯pta方法在快速生成裂缝半长概率估计方面具有更强的通用性。这项研究证明了高斯pta模型在提供断裂半长确定性和概率估计方面的能力。分析的重点是对位于德克萨斯州西部Midland盆地的两口Wolfcamp井(即4H井和31H井)的生产数据进行检查。将RTA模型得到的结果与通过独立速率-瞬态分析和微震填图得到的半长估计进行了比较。因此,本文提出了一种基于先前未开发的裂缝半长估算分析方法的创新方法,并通过对新方法与传统RTA解决方案的综合比较分析提供了补充证据。
方法
我们的团队进行了这项研究,以检验最近开发的gpt方法在确定水力裂缝半长(Weijermars 2022a)方面的适用性。利用高斯压力瞬态分析(PTA)对页岩储层水力裂缝半长进行了评价,并与传统的rta方法进行了对比。在油气工业中广泛应用于水力裂缝半长计算,选择经典的rta法作为基准技术。本节第一部分介绍的工作流程应用于位于Wolfcamp地层(Midland Basin, West Texas)的两口页岩井(井4H和井31H)。
工作流
图1描述了采用高斯压力瞬变(GPT)方法对Wolfcamp页岩地层的两口井进行水力裂缝半长确定性和概率性评估的工作流程。
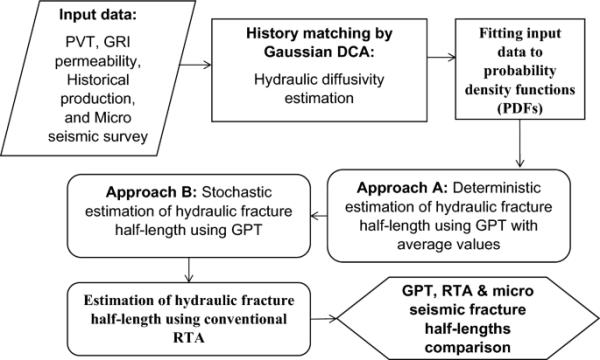
使用GPT方法评估水力裂缝半长(确定性和概率性)的工作流程
该工作流程首先收集所有必要的输入数据,包括流体和岩石性质、历史生产数据以及在水力压裂阶段记录的微地震调查数据。然后使用高斯dca方法获得水力扩散系数参数,该参数是应用gpt模型确定水力裂缝的确定性和概率半长的重要输入。利用传统RTA和微震解释的裂缝半长,验证了基于gpt的pta模型的结果。
输入数据
该研究结合了井数据,包括流体分析、岩石物理岩心分析、水力压裂过程中的微地震监测以及随后的历史生产数据,估计了水力裂缝半长。通过对相关数据集生成的输入数据分布进行概率抽样,获取关键参数的不确定性范围。下面简要介绍所使用的相关数据集。
PVT分析
页岩油储层pvt测试使用的数据是粘度和油层体积系数。使用油藏和井筒条件之间的平均粘度值。当原油从储层状态(油藏气泡)被提升到地面储罐状态(STB)时,油层形成因素考虑了体积变化。表1显示了每口井的相关PVT测试值。
页岩岩心分析
在页岩岩心分析过程中测量破碎页岩的渗透率,这是后续估计裂缝半长的重要输入。某服务公司采用新鲜、破碎、20/35目当量试样的压力衰减计算基质渗透率。在我们的研究中,两口井的渗透率数据集都使用概率分布函数进行拟合,并使用@Risk确定最佳拟合分布。根据赤池信息准则(AIC),威布尔概率分布函数对两口井的原始数据进行了最佳拟合。图2a, b。
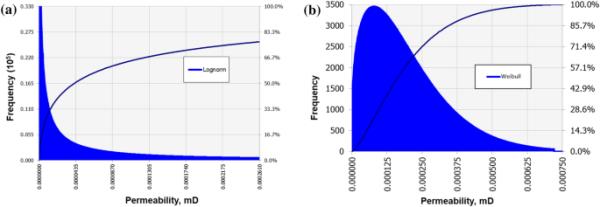
渗透率概率密度函数(a) 4H(118个样本容量)和(b) 31H(95个样本容量)
历史匹配生产数据
研究分析的两口井均为Wolfcamp页岩地层的水力压裂井,生产时间超过两年。使用高斯DCA(根据Eq. 1)对生产数据进行历史匹配,以估计储层水力扩散系数(Dh),这是唯一未知的参数,初始产量qi假设为1 STB/天。利用Microsoft Excel的Solver插件进行历史拟合,得到日产量残差平方和误差最小的水力扩散系数回归:
(2)4H井共完成33级,每级射孔3个射孔簇。原始储层压力为4680 psi,井底储层压力保持在1000 psi。假设储层厚度为100英尺。在历史匹配中使用了四年的日产量,以建立最适合历史生产数据的扩散系数参数(Chakra & Saraf 2015)。4H井48个月的日产量数据与高斯DCA模型进行了历史匹配;得到的最佳拟合dca曲线如图3a所示。该井的水力扩散系数约为0.02267立方英尺/天。
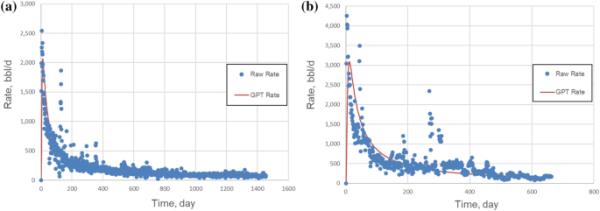
高斯DCA模型上的产量历史匹配(a)井4H(和(b)井31H
井31H有23个月的日产量数据,也用于估算水力扩散系数。原始油藏压力为5850psi,而井底压力保持在1000psi。该井的产层厚度为100英尺,共进行了36级压裂,每级压裂5个簇。23个月的日产量数据采用高斯DCA模型进行拟合,为最佳历史拟合提供最小的平方误差;相应的水力扩散系数为0.02178 ft2/天。表2中列出的扩散系数参数对于后续使用GPT模型估计裂缝半长至关重要。
微震的映射
微震监测是利用注水致裂引起的微震现象进行监测的技术。它与自然地震相似,但强度较低。微地震监测可以实时测量压裂过程中产生的裂缝的高度、长度、方向、几何形状和空间结构(Zou 2017)。3口邻井在31H井附近记录了微地震活动,并在4H井进行了直接监测。
微震监测发生在裂缝形成和扩展至最大值时。4H井的裂缝长度如图4所示,这是由监测井的微地震剖面生成的直方图。图5为4H井压裂过程中压裂后岩石体积的侧视图。之前使用基于复杂分析的流动模型详细分析了4H井周围的流体泄放情况(Weijermars等,2017a, b)。图6显示了31H井的邻井炮管视图。这些井距离31H井的井口仅3.5英里。
4H井每级微震裂缝长度直方图(a)长度不对称(b)总微震长度
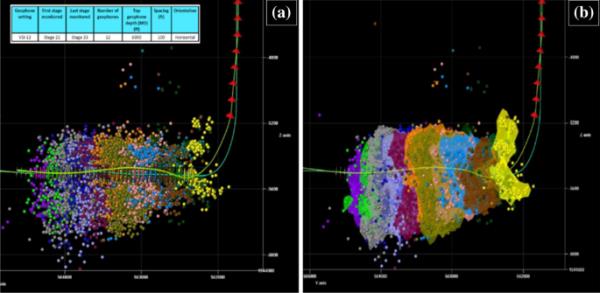
4H井增产体积微震侧面图。左图(a)为按阶段着色的信号;右图(b)是舞台的云色
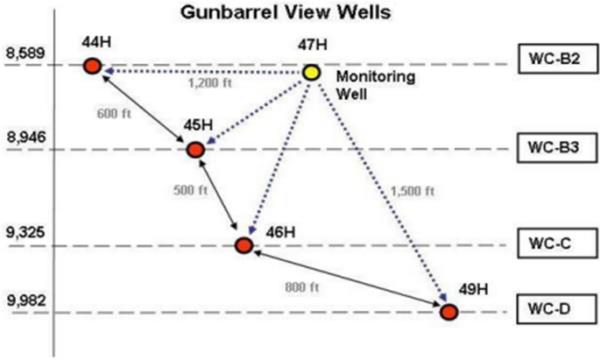
邻井(44H、45H和46H井)
井31H、井44H、井45H和井46H的分支位于同一个着陆区(Wolfcamp C-D),趾部间距仅为1.5英里。44H、45H和46H井的垂直井距为350英尺,水平井井距为375英尺。44H、45H和46H井的裂缝长度如图7所示,这是由监测井的微地震剖面解释的直方图。
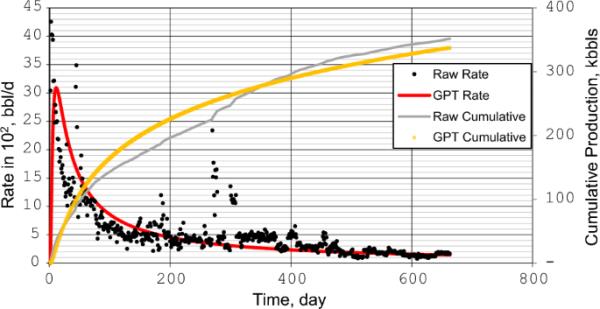
实测31H邻井(44H、45H、46H)微地震监测裂缝长度直方图
此前,46H井单段5条水力裂缝周围的3-D排水岩石体积是根据历史匹配的生产数据再生的(Parsegov et al. 2018)。表3总结了从微地震调查中估计的裂缝半长。由于44H井监测的压裂段数量有限,因此只使用了45H井和46H井的平均裂缝半长(图7)。
GPT-equations
Weijermars(2021)推导了多孔介质中流体流动的高斯压力-瞬态解,并将其作为递减曲线分析方法。在本研究的背景下,gpt模型可以通过使用历史产量回归来估计水力裂缝半长:
(3)式中qr(t)为t时刻的产量,Dh为水力扩散系数,2A为裂缝两侧的面积,k为基质渗透率,为流体粘度,P0为原始油藏压力,BHP为井底压力,x为到裂缝面的固定距离(如果使用现场装置,则为1英尺)
(4)应用同时考虑产出流体可压缩性并替代裂缝半长Yf的式(4a,b),可将式(3)改写为:
(5)式(5)将井流量与水力裂缝半长联系起来,可用rta法估计线性流动参数。转换因素C1, C2, C3都需要在单位工作时,与qr桶/天(t), t在天,Dh ft2 /天,2在ft2, k在mD, P0和必和必拓在psi, x = 1英尺,cPoise(等于mPa.s), B是石油储层的地层体积系数桶/机顶盒,n是骨折的总数,h代表储层厚度在英国《金融时报》,和C1, C2, C3转化因素领域单位0.178108桶/发生,1.06235 e-14 ft2 e-12 psi / mD和1.67868。天/ cPoise,分别。
重新排列Eq.(5)得到Eq.(6),本文采用该公式对断裂半长进行随机建模:
(6)GPT-Approaches
根据前几节介绍的gpt模型,评估了两种方法(A、B)来估计水力裂缝半长。方法A是确定性的,而方法B使用蒙特卡罗模拟对输入参数进行概率采样,并对裂缝半长进行历史匹配。使用蒙特卡罗模拟对输入数据进行随机采样(使用Microsoft Excel的Palisade@Risk插件执行),以考虑确定裂缝半长时的不确定性。
方法A:水力裂缝半长的确定性估计
在这种方法中,使用历史产量和Eq.(6)对裂缝半长进行历史匹配。从概率分布函数中,取所有方程参数的平均值,而不考虑不确定性。将裂缝半长平均值与传统rta分析和微地震测量裂缝半长进行比较。表4列出了这种方法中用于历史匹配的参数。在方法A中,我们从不使用完整的簇数;我们假设只有70%的射孔产生水力裂缝,即4H井为69,31H井为95(表4)。
方法B:水力裂缝半长概率估计
利用式(6)对输入值进行随机采样,利用历史产量估算裂缝半长。由于生产率和相应的时间是密切相关的,因此在抽样时考虑了它们之间的相关性。对于所有井,渗透率均考虑为100nd。将所得裂缝半长概率分布函数均值与传统RTA分析和微地震监测裂缝半长进行了比较。表5列出了此场景中使用的输入参数PDF特征。
在方法B中,对输入数据进行采样时,总簇数的成功率为70-100%;我们有效地使用了70%到100%之间的概率分布。我们没有使用完整的簇数,因为我们假设只有70%的射孔作为水力压裂的最小射孔数。对于方法A,我们在4H井使用69-99裂缝,在31H井使用95-136裂缝。
目录
摘要 介绍 方法 结果 讨论 结论 缩写 参考文献 作者信息 道德声明 搜索 导航 #####结果
使用所提出的方法(第0节)用gpt方法估计裂缝半长。gpt方法的结果将首先给出,然后是微地震和rta方法。两口井都将显示A方法的结果,然后再显示B方法的结果。
方法A: 4H井水力裂缝半长确定性估计
该方法通过两种情况确定地估计水力裂缝半长。利用式(5)将日率数据与高斯模型进行匹配。图8为历史匹配的递减率和累计递减率。利用实验室测量数据,采用历史拟合法计算水力裂缝半长。可以看出,考虑到有噪声的生产数据,历史匹配是可以接受的。由于停产时间较长(超过10小时),特定天的生产数据被排除在历史匹配之外。该井4H的历史匹配中省略了近48天的生产异常值。
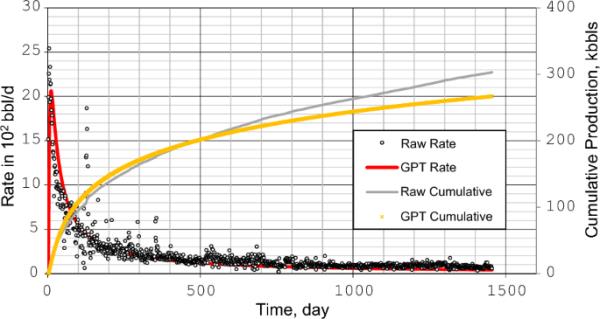
使用gpt方法对4H井的日产量和累积产量进行历史匹配
首先,从现有报告中获得PVT数据,以确定合适的FVF和粘度值。由于测量的流量是地表条件下的流量,必须转换成油藏条件下的流量,因此本方法考虑了油藏条件下的流量流场,如表6所示。由于我们只关注从储层到井底的流动,因此将考虑储层和井底压力条件之间的平均值。因此,利用储层条件(图1)FVF与储层和井底条件下的粘度相结合,估计了两个Yf值。表7总结了4H井采用A方法计算裂缝半长值的结果。
取两个确定性yf值(表7)的平均值,得到一个参考值,稍后将用于比较目的。4H井的平均裂缝半长为217英尺。
方法A: 31H井水力裂缝半长确定性估计
同样的程序应用于井31H。图9描述了日产量和累积产量的历史匹配图。如生产报告所述,由于与技术干预相关的不定期停产,在这种情况下,历史匹配不如前一口井好。例如,从图3b的历史产量可以看出,该井从第307天到第339天没有生产。此外,在我们的历史匹配中不考虑生产中断超过10小时的天数。对于井31H,从生产历史中省略了78天。

利用gpt方法对31H井的日产量和累计产量进行历史匹配
对于这口井,需要多个粘度值(例如井底和油藏条件值)。表8列出了不同压力下FVF和粘度的完整记录。表9显示了利用储层FVF以及油藏和井底条件下的粘度计算Yf结果的总结。对于即将进行的比较,取两个yf值的平均值,确定的参考值为177英尺。
方法B: 4H井水力裂缝半长概率估计
该方法利用输入分布对水力裂缝半长进行概率估计。利用输入的最佳拟合分布,应用式(6)来估计Yf的概率分布。为了以概率方式估计Yf,使用excel @Risk插件将一些输入参数拟合到分布中。考虑到输入之间的相关性,我们定义了流速(qw)和时间(t)的关联矩阵,因为它们之间存在很大的相关性(如图8的衰减曲线所示)。此外,FVF和粘度数据用于确定储层和井底条件之间的分布范围。表10显示了有关输入参数的最佳拟合分布。
现在根据Eq.(6)用一些离散值和一些概率值定义@Risk Output函数。对最终的Yf进行概率估计,如表10所示。此外,该方法报告的值包括P10、P50、P90和用于比较的平均值,如表11所示。
方法B: 31H井水力裂缝半长概率估计
同样的方法应用于井4H。然而,由于我们处理的是不同的井记录,输入参数的拟合分布有很大的不同(图10)。所使用的输入参数分布汇总如表12所示。
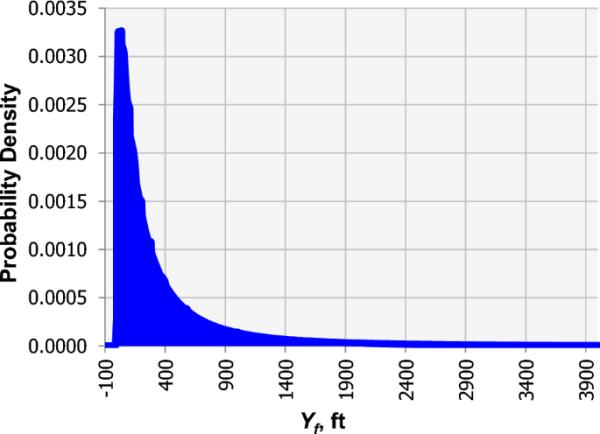
基于概率方法的4H井裂缝半长概率分布函数
进一步,用@Risk创建了时间和生产率的相关矩阵。图11显示了将方法B应用于井31H后得到的Yf的PDF。与Well 4H类似,报告了Yf分布的P10、P50、P90和平均值,如表13所示。
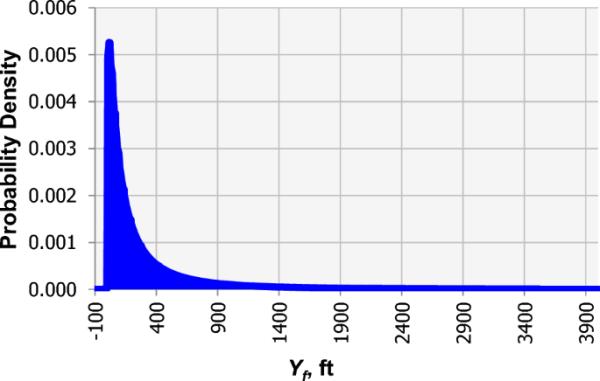
基于概率方法的裂缝半长概率分布函数
Micro-Seismic结果
本节将总结第0节所示的微地震数据,以验证GPT方法。表14包含了两口井的平均Yf值。必须强调的是,记录的微地震值高估了实际裂缝长度,并被视为其他方法的上限。
RTA-Results
速率瞬态分析(RTA)是一种用于分析页岩气井随时间变化的生产行为的方法。它包括使用压力、流量和生产数据来创建描述油井性能的数学模型。然后使用该模型来预测未来的油井行为,例如该井将以一定的速度持续生产多长时间,以及在井的生命周期内将采收率多少。RTA被认为是优化生产、制定完井和增产决策的重要工具。
速率-暂态分析(RTA)基于压力暂态方程的常规试井解,假设井速恒定,并提供了直井。当将RTA应用于水力压裂井时,可以使用Wattenbarger等人(1998)的解决方案,该解决方案假设线性流动和无限裂缝导流能力。在应用RTA时,使用产量来标准化油藏与井底压力之间的压降(p-pwf)。然后将归一化压降和物料平衡时间(tmb)用于rta图中进行交流表征(Nashawi和Malallah 2006)。为了识别不同的流动状态,建议使用测井-测井诊断图和降压/油率导数函数。一般来说,在无限导流水力压裂井中,诊断图上斜率为1 / 2的线性流型是主要的流型。这需要构建(1)(p)/qo对(tmb)的诊断对数-对数图,以及(2)对t的对数-对数图(图12b)。然后可以将流态确定为绘制数据的切线斜率的函数(Ibrahim and Wattenbarger 2005;Dheyauldeen et al. 2022)。最后,需要通过绘制归一化压力差与物料平衡时间的平方根来构建线性流态的专门图。在笛卡尔曲线中,可以估计出一条斜率为m的直线,由直线斜率m可以计算出(Wattenbarger et al., 1998):
(7)式中,Ac为总裂缝表面积,反映了产液的有效面积,分别为地层孔隙度、流体粘度和总压缩性。T是温度,k是地层渗透率。已知裂缝数(Nf)和裂缝高度(Hf),则平均裂缝半长(Yf)可由下式估算。
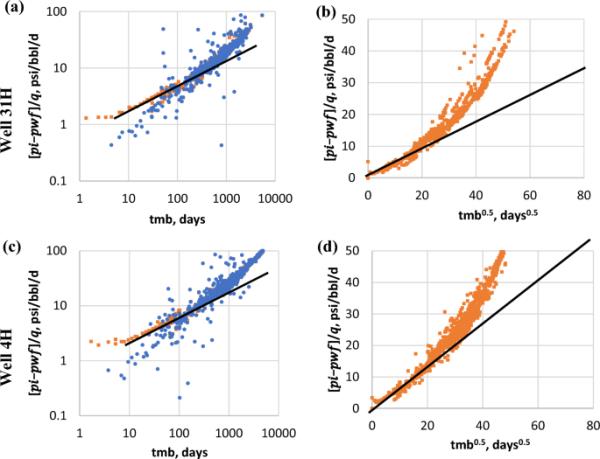
对于31H和4H井的RTA分析,左列(a)和(c)表示归一化压力差除以速率与物料平衡时间的诊断图,右列(b)和(d)表示线性流动状态的RTA专用图
(8)这些RTA方法应用于所研究的两口井。图12显示了通过测井诊断图和专门的笛卡尔图对两口井进行的RTA分析。结果表明,4H井的裂缝半长略长于3H井。据估计,31H井和4H井的裂缝半长分别为293英尺和200英尺。
下载原文档:https://link.springer.com/content/pdf/10.1007/s13202-023-01680-9.pdf

