摘要

深度学习是侧信道分析的一个强大方向，因为它可以在相对较少的攻击痕迹下破坏受对策保护的目标。尽管如此，有必要进行超参数调优以达到强大的攻击性能，这可能远非微不足道。除了来自机器学习领域的许多选择外，近年来还引入了专门用于侧信道分析的神经网络元素。损失函数用于计算实际输出与期望输出之间的误差或损失，是神经网络最重要的元素之一。由此产生的损失值指导与深度学习神经网络的神经元或过滤器之间的连接相关的权重更新。不幸的是，尽管是一个高度相关的超参数，但在不同的损失函数之间没有关于它们在侧信道攻击中的有效性的系统比较。这项工作提供了在SCA上下文中不同损失函数的效率的详细研究。我们评估了机器学习中常用的五种损失函数和专门为SCA设计的三种损失函数。我们的结果表明，特定于sca的损失函数(称为CER)在大多数评估设置中表现非常好，并且优于其他损失函数。尽管如此，分类交叉熵仍然是一个很好的选择，特别是考虑到神经网络架构的多样性。

1 介绍

侧信道分析(sca)是针对加密算法的一种强大的实现攻击。侧信道分析通常分为直接攻击和两阶段(分析)攻击。分析攻击假设一个“打开”的设备(或它的副本)。通过建立基于该设备泄漏的模型，攻击设备的密钥恢复只需要少量的测量。今天，分析攻击的一些最强大的代表来自深度学习领域[4,19,31]。文献表明，此类攻击可以破坏配备对策的目标，但需要仔细调整超参数以对抗此类保护机制[12]。不幸的是，由于深度学习架构的复杂性，找到最佳的超参数组合是一项具有挑战性的任务。

损失函数是一种可调超参数，在深度学习模型的训练中起着核心作用。它们用于计算实际输出与期望输出之间的误差或损失;结果值被传播回学习，即更新与深度学习网络的神经元或过滤器之间的连接相关的权重。损失函数的选择会影响得到的深度学习模型的性能[10,33]，这在SCA领域也得到了认可。

1.1 相关的工作

近年来，由于深度学习在不同攻击设置下的灵活性和强大的攻击性能，深度学习在SCA上下文中变得越来越流行[4,12,16,17,23,28,36]。其中许多工作都集中在优化网络架构以增加模型的攻击能力。例如，Zaid等人[36]提出了一种为SCA寻找性能良好的体系结构的方法。Kim等人[12]也研究了不同的建筑选择和噪声的影响。最近，人们提出了不同的框架来自动化网络调优[24,32]。然而，所有这些工作都有一个共同点，即没有考虑使用的损失函数。当他们首次探索将深度学习技术用于SCA[16]时，作者提到分类交叉熵或均方误差是常用的损失函数。后来关于SCA深度学习的研究似乎只使用分类交叉熵[3,19,36]或均方误差[18,28]。

最近，专门针对SCA上下文提出了三种新的损失函数:排序损失(RKL)[35]、交叉熵比(CER)[37]和焦点损失比[11]。详细的讨论可以在2.3节中找到。这些论文将新提出的损失函数与分类交叉熵进行了比较。不幸的是，这些比较的范围是有限的，并且只测试了单一的体系结构或泄漏模型。

据我们所知，在不同的体系结构、泄漏模型和数据集上，还没有对常用的损失函数(如分类交叉熵、均方误差或铰链损失)和这些新的基于sca的损失函数进行广泛的比较。

1.2 动机和贡献

为了验证各种提出的损失函数的通用性，迫切需要对不同攻击设置中的不同损失函数进行系统评估。在这项工作中，我们的目标是填补这一空白。更准确地说，我们系统地比较了常用的损失函数和新的特定于sca的损失函数在四个公开可用的数据集和两种常用的泄漏模型上。我们从多个角度评估性能:攻击性能(猜测熵)，神经网络类型和大小，以及所需的训练时间。我们的研究结果显示了最近提出的FLR和CER损失函数的出色性能，特别是当使用Hamming Weight泄漏模型[11,37]时，由于类别不平衡和机器学习指标缺乏可靠性，该模型可能代表一个具有挑战性的场景[22]。排名损失是最近提出的另一个损失函数，它的性能与特定的神经网络架构密切相关:它可能在某些特定的设置中表现最好，但在大多数情况下，FLR和CER是更好的选择。最后，在基于深度学习的SCA中，分类交叉熵是一种常见的选择，由于其低计算开销和不同神经网络架构的通用性，被确认为一种竞争选择。

2 背景

2.1 剖面侧通道分析

对于侧信道分析，假设攻击者拥有与要攻击的设备相同(或至少相似)的克隆设备。攻击者使用来自分析设备的泄漏度量(带有已知的标签信息，即要攻击的秘密变量)来构建分析模型。然后，攻击者使用被攻击设备的Q值来推断秘密信息。分析攻击的演示如图1所示。根据分析技术的不同，可以构建不同类型的分析模型:模板攻击模板和机器学习模型。本文的重点是机器学习模型。

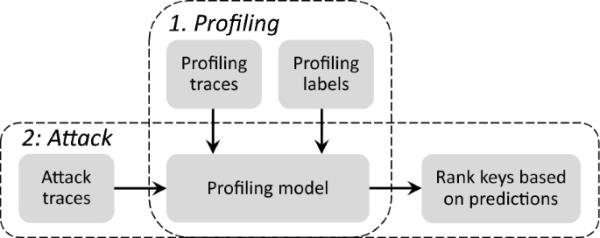
侧信道攻击

2.2 深learning-based侧信道分析

监督式机器学习的目的是基于输入输出对的例子，学习一个将输入映射到输出的函数。监督学习分为两个阶段:训练和测试。这对应于分析SCA阶段，通常表示为分析和攻击阶段。

数据集被定义为侧通道跟踪(测量)的集合，其中每个跟踪都与输入值(明文或密文)和密钥相关联。我们将数据集划分为不相交的子集，其中训练集有M条轨迹，验证集有V条轨迹(因此，)，攻击集有Q条轨迹。

1. 1.

   剖析阶段:目标是学习(参数向量)最小化由大小为M的数据集T(即剖析(训练)集)上的损失函数L表示的经验风险。

2. 2.

   攻击阶段:目标是对类做出预测

   其中表示被攻击设备上的秘密(未知)密钥。使用模型f对攻击集进行预测的结果是一个二维矩阵P，其维度等于(其中c表示类的数量)。然后将任意关键候选k的累积和S(k)用作最大对数似然区分符:

   （1）

   该值是由密钥k导出并通过加密函数CF和泄漏模型l输入的类v的概率。

在SCA中，攻击者的目标是泄露密钥;标准的绩效评估指标是成功率(SR)和猜测熵(GE)[27]。这项工作使用猜测熵度量来估计攻击性能。更具体地说，给定攻击阶段的Q跟踪，攻击以概率递减的顺序输出密钥猜测向量:最可能和最不可能的密钥候选。

2.3 损失函数

在本节中，我们讨论将在实验中使用的损失函数。表示预测向量，表示真值向量。最后，用to表示第i个真值，用to表示对应的预测值。

2.3.1 均方误差

最简单的损失函数之一是均方误差(MSE)[26]。MSE的计算方法是将预测向量的元素与真实值的向量的元素之间的两两平方差的平均值以一热格式计算:

（2）

式中，M为训练样本个数。MSE及其变量已被用于解决回归问题(因此，函数的输出f是连续的)[26]。对于每个样本，无论样本属于哪一类，损失都是均匀计算的。通过最小化损失，我们减少了预测和真实标签之间的距离。MSE也可用于分类问题[10]，并已在SCA上下文中使用，如前所述[29]。

MSE的一种变化是均方对数误差(mean squared logarithmic error, MSLE)[1]。MSLE不是直接使用向量之间的差，而是通过对真实值和预测值应用自然对数的差来计算。与之相比，MSLE对数据中的异常值不太敏感。

（3）

最后，我们考虑双曲余弦(logcosh)的对数作为损失函数。与MSE相比，Log cosh loss与MSLE一样，对异常值也具有鲁棒性[30]:

（4）

2.3.2 分类损失

分类任务的实际标准损失函数是分类交叉熵，有时也称为负对数似然、软最大损失、对数损失或交叉熵。它已用于各种分类任务[8,13,34]，也常用于SCA[3,12,16,17]。交叉熵是对两个分布之间差异的度量。最小化交叉熵，它表示深度学习模型建模的分布与类的真实分布之间的差异，因此应该改善神经网络的预测:

(5)

其中c表示类的数量。

另一个用于分类的损失函数是(分类)hinge损失[5]。铰损增大了正确类预测概率与预测概率最高的错误类预测概率之差:

（6）

2.3.3 自定义SCA损失

最近，提出了三个特定于sca的损失函数。一种是Zaid等人[35]提出的rank loss (RKL)函数。排名损失使用模型的输出分数和将softmax激活函数应用于这些分数所产生的概率。排名损失背后的想法是在应用softmax函数之前比较正确键字节和分数向量中其他键字节的排名:

（7）

其中，为模型处理训练样本生成的每个关键假设的得分向量，为所有可能的关键值的集合，为正确的关键，s(k)为关键猜测k的得分，通过查看k在中的排名来计算。最后是一个参数，需要根据不同的攻击设置进行设置。排名损失函数的实现由[35]在GitHub上提供。注1:这是RKL的一个关键参数。我们基于随机搜索优化这个超参数。

另一个自定义损失函数是Zhang等人提出的交叉熵比(CER)损失[37]。作者将CER作为SCA度量引入，以评估SCA上下文中深度学习模型的性能。同时，该指标可以直接作为损失函数，使用一组洗牌:

(8）

其中cce是分类交叉熵。表示具有真实概率的向量，正确类为1，其他所有类为0，每个类随机洗牌(洗牌)。变量N表示要使用的洗牌集的数量。作者没有提供N的值，但指出增加N应该增加度量的准确性。在我们的第一个实验中，为了平衡计算复杂性和准确性的潜在提高，我们使用。

最近提出了焦损比(FLR)损失函数[11]，它综合了焦损函数[14]、分类交叉熵和CER的优点。FLR的计算公式为:

（9）

与CER对齐，分别表示真实标签和洗牌标签;cce是分类交叉熵，N是要使用的负样本数。引入了对类进行加权，并分别对分子和分母强调硬样本。在本文中，我们按照原论文对这三个超参数的选取[11]，分别将、、和N设为0.25、2和3。

2.4 数据集

2.4.1 ASCAD固定密钥(ASCADf）

ASCAD数据集是通过运行屏蔽AES-128的ATMega8515进行测量生成的，并被提议作为SCA的基准数据集[3]。该数据集由50,000个分析跟踪和10,000个攻击跟踪组成，每个跟踪由700个特征组成。在本文中，我们将分析跟踪的数量设置为50,000。在攻击阶段，我们使用多达2000个跟踪。分析集和攻击集都使用相同的固定密钥。我们将此数据集表示为ASCADf。我们攻击第三个密钥字节，因为它是第一个掩码字节。本文考虑了汉明权重(HW)泄漏模型和身份(ID)泄漏模型。该数据集在ASCAD GitHub存储库上提供。脚注2

2.4.2 ASCAD随机密钥(ASCADr）

ASCADr数据集由200,000个分析和100,000个攻击痕迹组成，每个特征由1400个特征组成。与ASCADf数据集不同，分析集中使用的键是可变的。在本文中，我们将分析跟踪的数量设置为50,000。在攻击阶段，使用3000条trace。我们攻击第三个密钥字节，因为它是第一个掩码字节。我们将考虑汉明权重(HW)和身份(ID)泄漏模型中的攻击。ASCADf数据集可以在ASCAD GitHub存储库中获得。脚注3

2.4.3 ctf2018 (CHES_CTF）

该数据集于2018年为加密硬件和嵌入式系统会议(CHES)发布。目标实现是在32位STM微控制器上执行的掩码AES-128加密。在我们的实验中，我们对包含固定键的训练集使用了45000条轨迹。验证集和测试集各由5000个跟踪组成，其中我们在攻击阶段使用了3000个跟踪。我们考虑了一个预处理的数据集版本，其中每个跟踪由2,200个特征组成。与ASCAD数据集不同，训练和验证集中使用的密钥与测试集的密钥不同。我们攻击第一个密钥字节，并考虑汉明权重和身份泄漏模型。

2.4.4 DPAv4.2

数据集包含从掩码AES-128软件实现中获得的侧信道测量值。该对策基于RSM(旋转s盒掩蔽)。原来包含80000条线路，分为16组，每组5000条。每个组都用一个单独但固定的键定义。每次测量有1,704,046个样本。在这项工作中，我们对密钥字节12的二阶泄漏间隔进行了侧信道分析，密钥字节12的秘密份额具有最高的信噪比。攻击间隔从样本305000开始，到样本315000结束。最后，我们对连接的间隔应用重采样过程，重采样窗口为10，步长为5，每次测量得到2000个样本。我们在汉明权重模型和身份泄漏模型中攻击数据集。

2.5 泄漏模型

本文考虑了两种泄漏模型:

1. 1.

   汉明权值(HW):攻击者假设泄漏量与敏感变量的汉明权值成正比。当考虑AES密码(8位S-boxFootnote 6)时，这种泄漏模型会导致9个类别。

2. 2.

   ID (Identity):攻击者以密码的中间值的形式考虑泄漏。当考虑AES密码(8位S-box)时，该泄漏模型导致256个类。

目录

摘要 1 介绍 2 背景 3.实验装置 4 实验结果 5 讨论 6 有限公司 结论和未来的工作 笔记 参考文献 致谢 作者信息 搜索 导航 ＃＃＃＃＃

3.实验装置

几个不同的超参数，如层数和每层神经元的数量，每个神经元使用的激活函数和损失函数，都会影响深度学习模型的训练过程。通过选择具有特定训练超参数的单个模型，我们最终可能会得到某些超参数，这些超参数对一个损失函数的影响大于其他损失函数。如图2所示。除了损失函数和学习率外，每个模型都使用相同的超参数进行训练。当学习率设置为0.00001时(图2a)， CER损失表现最好，其次是CCE和RKL。然而，当学习率增加到0.001(图2b)时，导致GE收敛的损失函数CCE和RKL不再具有功能。同时，对于CER损失，性能甚至有所提高。因此，单一攻击模型和固定攻击设置的基准测试不能代表损失函数的一般性。知道了这一点，我们考虑以下场景来进行公平的损失函数比较:

除了学习率外，所有模型都使用相同的超参数进行训练。学习率对某些损失函数的模型性能影响较大。在学习率设置为0.001的场景中，CER损失的性能有所提高，而其他损失未能导致模型收敛到GE为1。给出了ID泄漏模型中ASCADf数据集的实例

我们通过随机搜索每个考虑的损失函数来执行超参数优化，以获得最佳表现的模型。更具体地说，我们执行以下步骤来选择和评估最佳模型:

1. 1.

   为每个损失函数生成、训练和测试100个随机模型。

2. 2.

   选择在猜测熵方面表现最好的模型。

3. 3.

   对所选模型进行10次训练和测试，以补偿随机权值初始化的影响。

4. 4.

   从这十个模型中，选择基于猜测熵的每个损失函数的中值模型。

5. 5.

   比较每个损失函数在猜测熵和训练时间方面的攻击性能。

我们决定展示中位数模型的结果，因为(1)它避免了异常值行为，无论是作为一个表现良好的模型还是一个根本不能收敛的模型;(2)不能保证任何被测试的模型都能完全表现为平均模型。

我们考虑两种架构类型:多层感知器(mlp)和卷积神经网络(cnn)。这两种类型的深度学习架构通常用于SCA，并且在以前的工作中显示出出色的结果[3,16,36]。对于每个数据集、泄漏模型和损失函数组合，我们部署了一个具有两个搜索范围的超参数搜索，从而产生不同的网络大小。在此基础上，我们可以研究不同模型学习能力下损失函数的训练效率。表1提供了小型MLP模型的超参数范围。对于较大的MLP模型，我们提供了如下表2所示的超参数范围[20]，以便在良好的性能和每个超参数的广泛可能值范围之间取得平衡。我们训练每个模型200次。了解到epoch的数量对模型的性能有很大的影响，我们引入了一个早期停止机制，当模型开始过拟合时终止训练过程。根据[25]中提出的方法，在训练过程中使用猜测熵来监控模型的性能。在优化器方面，由于Adam和RMSProp优化器表现良好[3,20]，这两种优化器都被认为是一种选择，自然，学习率的范围被扩大了。

对于CNN超参数，如表3和表4所示，我们再次定义了两个搜索范围。此外，如[9]所引入的，在输入层和每个卷积块之后应用批处理归一化层，如早期工作所做的那样，以提高cnn的性能[3,4,20]。

请注意，体系结构的大小与搜索空间大小并不直接相关。即使对于一个小的体系结构，也可以有很多可能性来构建它。

为了在不同的损失函数之间进行广泛的比较，我们定义了32种不同的攻击场景来对每个数据集进行比较。这些场景中的每一个都结合了一个数据集、一个泄漏模型、一个体系结构类型和一个网络搜索范围。

所测试的损失函数是在不同深度学习应用中常用的函数，以及专门为SCA开发的新型损失函数，将在2.3节中介绍。值得注意的是，当使用RKL进行随机搜索时，一个固定的(例如，原始论文中使用的值)可能会限制到特定的攻击设置。因此，在网络搜索过程中，我们将其作为一个需要搜索和优化的超参数。取值为:0.5、1、2、3、4、5、6、7、8、9、10。

两个数据集都使用预先选择的特征窗口，不再进行兴趣点的选择。有趣的是，我们注意到，直接应用原始特征或遵循早期的工作，将SCA特征缩放到0到1之间的值[15,35]，可能导致训练期间的损失值等于NaN，这表明有可能触发爆炸梯度问题:反向传播期间的梯度变得太大或太小。在最坏的情况下，它可能导致学习过程失败[21]。为了验证这一点，图3显示了其中一个模型在训练过程中每个epoch输入层的最大和最小梯度。梯度爆炸问题的原因可能来自几个超参数的组合，例如，激活函数、损失函数和预处理过程中使用的0-1归一化。例如，将所有特征值规范化为0到1之间的值，可以从分析跟踪中删除任何负值。激活函数的输出，如ELU[如Eq.(10)所示]等于所有函数的输入。这意味着输出是无界的，也就是说，它可以达到的大小没有限制。更重要的是，它还意味着，由于我们将值归一化为0到1之间的值，激活函数的输出将始终是正的(对于ReLU激活函数也是如此)。这会导致梯度过大，导致模型表现不佳甚至训练失败。

（10）

解决这一问题的方法有两种:(1)通过z分数归一化(标准化)对泄漏轨迹进行归一化;(2)在梯度过大或过小时进行裁剪。所有实验我们都采用第一种方法作为预处理方法。虽然攻击性能可能与使用0-1归一化时相似，但触发爆炸梯度问题的可能性可以大大降低。

4 实验结果

在本节中，我们将讨论上述每个实验的结果。我们将看看损失函数在通过随机搜索优化的模型上的性能。实验采用单个CPU和NVIDIA GTX 1080 Ti图形处理单元(GPU)，具有11 gb的GPU内存和3584个GPU内核。

4.1 ASCADf

我们首先考虑不同损失函数在ASCADf数据集上的性能。图4显示了分别使用小搜索空间和大搜索空间生成的每种场景中性能最佳的模型的超过100次攻击的猜测熵。达到猜测熵为零所需的攻击痕迹数量列在图的图例中。

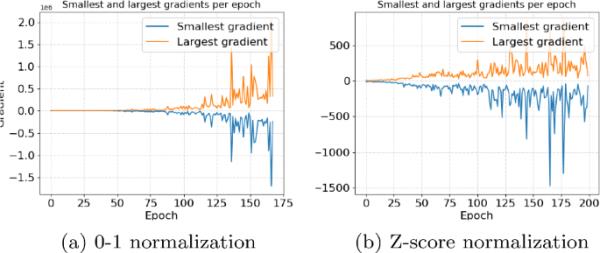
在中值MLP和HW泄漏模型中，经过不同预处理后，具有CER损失的模型训练时输入层梯度的最大值和最小值。梯度在0-1归一化时爆炸到很大的值，但在应用z分数归一化时则不会

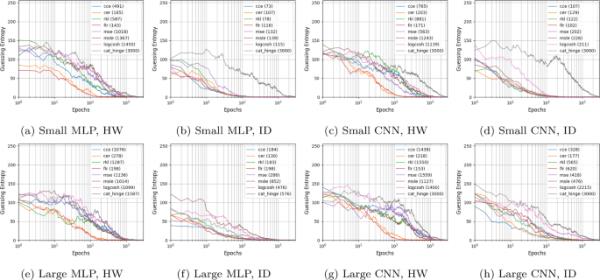
在ASCADf数据集上的最佳MLP和CNN模型的GE

首先，我们注意到ASCADf数据集容易受到具有各种攻击设置的SCA的攻击。大多数损失函数导致的模型可以在最佳性能的MLP和CNN架构下在不到1000个跟踪中检索到正确的密钥。此外，即使是通过随机搜索的简单超参数优化方法也可以提高攻击性能。例如，CER模型在不到300次跟踪中达到了1的GE，这与最先进的攻击性能相当[31,35]。此外，可以观察到，使用小型或大型网络架构可能会影响攻击效率，但不会显著改变不同损失函数的性能等级。

从结果来看，虽然不是最好的，但常用的分类交叉熵在这些场景中确实表现得非常一致。另一方面，由于在损失函数中引入了负样本，CER和FLR几乎总是前两个损失函数。在CER方面，值得注意的是，Zhang等[37]只在HW泄漏模型，即不平衡数据上测试了该损失函数。我们的研究结果表明，CER损失也非常适合于内径泄漏模型。对于FLR，强调硬样本使其在大多数评估情况下甚至优于CER。因此，我们可以得出结论，当考虑ASCADf数据集时，损失函数的最佳选择是FLR损失。令人惊讶的是，排名损失(RKL)在测试场景中的表现不太一致。Zaid等人[35]将RKL函数与分类交叉熵和CER损失进行了比较，指出当为每个类适当调整超参数时，RKL的性能优于这两个函数。然而，他们只比较了单一的CNN架构，并考虑了ID泄漏模型[35]。我们的研究结果证实，RKL与ID泄漏模型相比，与ASCADf数据集的HW泄漏模型效果更好。然而，除了RKL表现最好的两个测试场景(图4d)外，它的表现总是比CER和FLR损失函数差。

在讨论这些结果时，必须指出的另一点是所需的训练时间。当所有其他超参数相同时，FLR、RKL和CER损失函数与其他损失函数相比明显更慢(训练速度时间)。在RKL的情况下，训练时间较慢的原因是两两比较，这是损失的一部分。这部分损失是通过将正确密钥的秩与所有其他猜测的密钥进行比较来计算的。当考虑HW泄漏模型(输出由9个类组成)时，这会对训练时间产生影响，而当使用ID泄漏模型(有256个输出类)时，影响更大。FLR和CER损失的训练时间增加也是由于这些损失函数的构造方式。

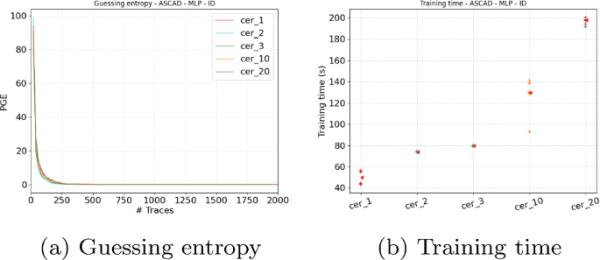
例如，计算CER的方法是将分析轨迹上的交叉熵除以N倍带有洗牌标记的分析轨迹集的平均值。在洗牌轨迹上计算交叉熵N次会导致比其他损失函数更慢的训练速度。然而，如图5所示，不同的N值给出的结果大致相同，其中表示达到猜测熵为零所需的攻击轨迹数。此外，对于较低的值，如或，与分类交叉熵等相比，训练时间没有明显差异，而GE的性能仍然有所提高。FLR也有类似的观点，因为它使用的N值很小，对训练时间的影响可以忽略不计，但却提供了优异的性能[11]。

使用不同的N值对具有CER损失的优化模型的熵和训练时间进行猜测

表现最差的损失函数是分类铰链损失。一个可能的原因是，当考虑HW泄漏模型时，学习率低，类数少。此外，如果我们看一下2.3节所描述的分类铰链损失的定义，则损失的负部分是基于概率最高的错误类别计算的，即最大的分类误差。不幸的是，有许多错误的类(255)，只有一个具有ID泄漏模型的正确类。由于权值的随机初始化，在训练开始时，来自错误分类轨迹的损失将保持在大约1，并且损失变化的主要贡献必须来自正确分类的示例。

总的来说，当考虑ASCADf数据集时，如果对手使用随机搜索进行超参数调优，考虑FLR和CER损失函数，由于它们对各种攻击设置的弹性，可以增加模型检索密钥的能力。事实上，它们明显优于具有分类交叉熵、排序损失和其他损失函数的模型。

4.2 ASCADr

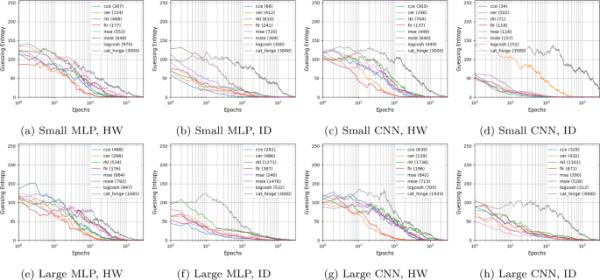
接下来，我们看一下ASCADr数据集上的结果。图6显示了具有不同搜索范围的最佳性能模型上的GE性能。

对于在ASCADr数据集上进行的实验，我们看到的结果与ASCADf数据集上的结果相当。在大多数情况下，使用FLR和CER损失训练的模型表现最好，其次是使用分类交叉熵训练的模型。在大多数情况下，RKL的表现不如CCE。最后，在大多数情况下，分类铰链损失表现最差。令人惊讶的是，CCE在使用ID泄漏模型时表现最佳(例如，图6b, d)，这表明它在使用较小网络大小的输出节点时表现优异。对于ID泄漏模型或更大的网络规模，更复杂的损失函数，如FLR和CER，在大多数情况下优于CCE。

4.3 CHES_CTF

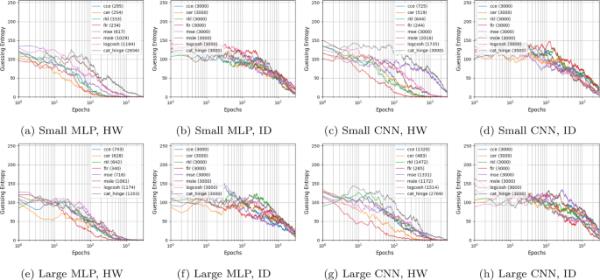
CHES_CTF数据集的结果如图7所示。与ASCADf和ASCADf数据集类似，网络大小的差异可能会改变攻击痕迹的数量，以达到猜测熵为零。然而，它对不同损失函数的基准影响有限。与之前评估的数据集相比，CHES_CTF数据集需要更多的攻击痕迹来破坏目标。具体来说，HW泄漏模型比其对应模型导致更强大的攻击，这与文献[24,32]的结果一致。当观察每个损失函数时，尽管所有损失函数都会导致GE收敛，但在使用HW泄漏模型时，FLR和CER仍然是打破目标的前两个候选函数。当移动到内径泄漏模型时，由于其随机性，结果更难解释。尽管如此，CER和FLR仍然是最快实现GE融合的首选方案。CCE和RKL损失函数在GE性能方面处于中间位置。最后，分类铰链损失在所有考虑的损失函数中表现最差。

4.4 DPAV4.2

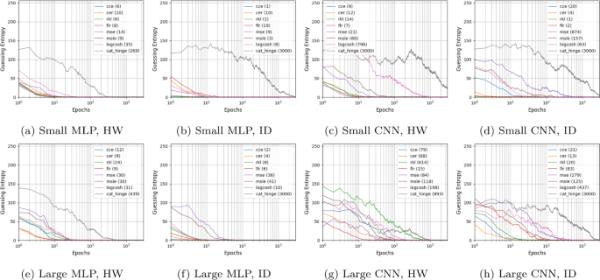
一般来说，与之前评估的其他数据集相比，DPAV4.2是最简单的数据集。较大搜索范围的结果如图8所示。许多损失函数可以在100个攻击轨迹内破坏目标。然而，人们可以观察到不同损失函数之间的性能变化。例如，当使用MLP和HW泄漏模型时，大多数损失函数在不到40道的情况下就破坏了目标(图8b, e)，而分类铰损失则需要十倍以上的攻击道，这与其他数据集的观察结果一致。另一方面，CCE、CER、RKL和FLR的性能变化较小是由于神经网络结构的变化。尽管如此，当使用CNN与HW泄漏模型时，FLR损失优于其他损失函数。

在ASCADr数据集上的最佳MLP和CNN模型的GE

在CHES_CTF数据集上的最佳MLP和CNN模型的GE

在DPAv4.2数据集上的最佳MLP和CNN模型的GE

下载原文档：https://link.springer.com/content/pdf/10.1007/s13389-023-00320-6.pdf