摘要

稳定拟映象的模空间中的约简分量到n维射影空间\(\mathbb {P}^n\)是指区域曲线光滑的轨迹的闭包。与在稳定映射的模空间中一样，我们证明了约简分量在2次上是光滑的。然后证明了X的\(\mathbb {P} n\)的2次次\(\ g3 \)的完全交X的稳定拟映象的模空间的虚基本环是用\(\mathbb {P} n\)的约简分量的基本环和\(<2\)模空间的虚环显式表示的。

1 介绍

计算五次三倍X的Gromov-Witten不变量由于其在镜像对称中的重要性而引起了数学家和物理学家的兴趣，而镜像对称主要研究Calabi-Yau三倍。克服这种计算的一种有效方法是将它们与嵌入X的GW不变量联系起来。然后我们对自然环面作用应用虚拟定位[23]来计算它们。我们将这个原理称为X的GW不变量和量子Lefschetz性质。

量子Lefschetz这个名字最初来自于0个虚环之间的公式:分别为稳定映射的模空间。上面有一个由通用曲线和通用图定义的相干层。在属0中，是光滑的，V是一个向量束。那么量子Lefschetz公式[29]断言

(0.1)

不幸的是，(0.1)并不适用于更高的属不变量[22]。所以我们需要更复杂版本的量子Lefschetz性质来解释高属不变量。

同时，已知GW与X的稳定拟映射不变量之间的显式关系为wall-crossing公式[14,16,40]。由于对于高属拟映射不变量，我们可能期望一个相对简单的量子Lefschetz性质，因此wall-crossing公式允许我们研究更简单的量子Lefschetz性质来计算GW不变量。例如，最初的量子Lefschetz公式(0.1)对1属拟映射不变量成立，因此它极大地帮助了1属GW不变量的计算[30]。

我们注意到，最近几年发展了几个有趣的量子Lefschetz公式，用于高格GW或拟映射不变量，或X的不变量与其他不变量之间的关系[1,3,5,7,9,10,11,17,18,20,30,33,34,41,43]。这导致了我们对高属不变量的一些实际计算[4,20,24,25,30,38,42]。在我们的论文中，我们想引入另一个关于2属拟映射不变量的量子Lefschetz公式。我们的公式(0.2)，(0.4)包含zinger型约简虚循环，这在以上任何文献中尚未对属进行研究。由于我们期望它有一些有趣的性质——比如可积性——我们希望我们的新公式能给研究高属不变量提供一些思路。

为了构造zinger型约简虚环，我们需要研究在稳定映射或稳定拟映射的模空间中(猜想地)支持环的约简分量。它首先在[26,39]中被提及，他们在那里研究了1属稳定图。后来[2,27]以不同的方式研究了2属稳定映射-[27]更接近于[26,39]的原始想法，而[2]使用具有Gorenstein奇点的曲线。虽然[2]研究了更一般的目标空间，但由于其在计算上的优势，我们遵循[27]的思想来构造我们的简化虚拟循环。

我们考虑更一般的情况。设为射影空间中的完全交点，其中。时，它恢复一个五次三重x。我们用g属的稳定拟映象的模空间表示，次为d，有k个标记点。使用通用曲线和地图

我们定义，其中是一个由权重d表示定义的束。让它成为开放子堆栈的闭包，它在其中消失

那么在第2.4节的固有基变换上，的固有变换是光滑的，那里是一个束。我们用与第j个标记点相关联的同义线束表示，它形成的部分，其中表示的相对对偶束。我们经常在整篇文章中省略下标j。

然后证明了Calabi-Yau 3-fold的量子Lefschetz公式。

定理1

当X是一个Calabi-Yau 3-fold时，我们在同调群中有一个等价，

(0.2)

使用的定义节，(0.2)的RHS中的第一项被定位到通过细化的欧拉类[21,section 14.1]Footnote 1，由section cutting out定义。RHS中的最后两项是通过嵌入的前推在Q(X)上的循环，

1. （1)

   ，

1. (2）

   ．

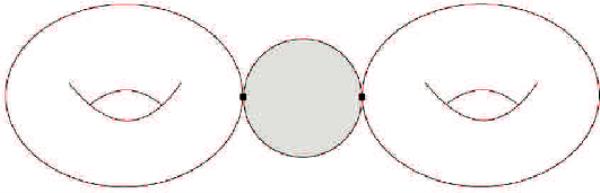
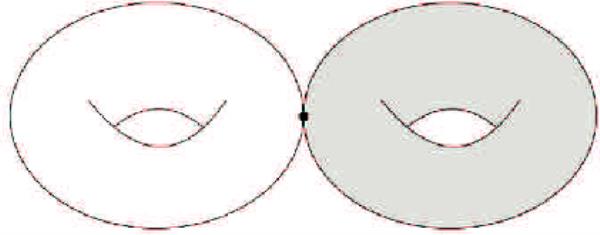
事实上，我们在(0.2)中有这些额外的项，因为Q(X)上的束不会在像上消失。注意，图像of包含在图像of中，但是图像of的秩会跳转到图像of上。这就是为什么在(0.2)中有两个额外的项。

这一捆不会在图像上消失

1. （3）

   ，

其中，两个求值映射相同的闭合子堆栈，

也所以它可能对公式有重要影响。也可能有另一个重要的贡献来自于它与像的交集。(请注意，它不会与的图像相交。)这些都是不完全消失的地方。因此，我们可能不会期望公式中有更多的额外贡献。实际上，我们有下面定理2中的公式对于一个一般的完全交集包括四个贡献。当X是Calabi-Yau三倍时，第三和第四个贡献消失，定理2作为特例得到定理1。

在陈述定理之前，我们引入了一些(Chow)上同类来简化陈述。通过Hodge bundle，我们定义了产品上的类，

当节点a是空的时，我们省略下标a。我们用i阶来表示。我们还定义了一个(Chow)同源类

(0.3)

使用对角线类。上的包定义为。

定理2

我们在Chow群中有一个等价，

(0.4)

在注释5.2中，我们解释了

，所以第四项并不奇怪。我们强调定理2是Chow群的结果，而定理1是同调的结果。

1.1 符号

对于空间的态射和Y上的完全复形，我们通常用衍生的回拉表示。我们有时把一个局部自由层E看作它的总空间。

我们用(或简单地)和为d的每个分量(起度作用)上的非负整数的预稳曲线的Artin堆栈来表示。类似地，或简单地，表示具有d度线束的曲线的Artin堆栈。具有d次因子的曲线的Artin堆栈表示为，或简单地表示为。

对于稳定拟映象的模空间或p域空间，我们用(i)的像表示。例如，(准映射的)求值映射是相同的。此外，除非需要解释，否则我们对嵌入的相关对象使用脚本(i)。例如，bundle on将用脚本(i)表示。

对于有两个下标的变量，我们说if适用于所有j，也适用于所有i和j。

2 quasimaps稳定,p-田地和计划

2.1 稳定quasimaps

有k个标记点的齐次多项式切出的完全交点的g属d次拟映象是一个三重(C, L, u)，其中C是有k个标记点的g属投影、节点、预稳曲线，L是C上的d次线束，并且是这样的一个截面

(1.1)

注意pair定义了一个映射。相反，当给定映射时，我们得到一对。因此，三元组(C, L, u)可以被认为是一个满足的对。如果一个拟映射满足稳定性条件，则它是稳定的

(1.2)

我们用，或简单地用Q(X)表示稳定拟映象的模空间。通过[13,15,35]，它适当地并配备了一个自然完善的障碍理论，使虚拟的基本类

(1.3)

定义，其中表示虚拟维度

X的稳定拟映射不变量被定义为在这个虚类上的积分。

准映射不变量的量子Lefschetz性质之所以更简单，是因为准映射在其定义域曲线上不具有少于两个特殊点(称为有理尾)的有理分量。

2.2 稳定拟映射p字段

我们在引言中已经看到，相干束可能不会消失。我们用，或者简单地用，它的对偶空间来表示

它的纤维是由Serre二象性。因为，其中(C, L, u)是与的稳定拟映象

回想一下，施加条件(1.1)定义了空间Q(X) from，而上述额外数据决定了from。我们称之为p场。

空间可能不适当，但仍有一个自然完美的阻碍理论，使虚拟基本类

定义。用通用曲线上的通用线束表示，定义相对于的对偶完全阻碍理论为

(1.4)

使用映射诱导，配对定义了共截面。Chang-Li在[6]中首先引入了p场空间和共分割，以找到一个较小空间的局部类，

(1.5)

使用共截面定位[28]。然后他们证明了X的GW不变量等于p域空间上定义的不变量。这个结果在[8,12,31,37]中得到了改进:本地化的类等于(1.3)中定义的类

(1.6)

2.3 定理2的证明方案

用(1.6)代替定理2中的命题。使用rather而不是Q(X)的一个优点是，它在局部是光滑空间的一个很好的切割。在第2节中，我们描述了在第2.4节中进行适当的碱基变化后的显式切割模型。利用这一点，我们计算3.2节中的固有法线锥，从而得到虚类的分解

(1.7)

请注意，指数'红色'，'(1)'，'(2)'和'(3)'反映了上面标记的几何原点。因此在节点识别态射的图像上得到支持，忽略p域。事实上，我们将在3.2节中研究它们是图像上的束。

然后在第4节中，我们证明了遵循原始量子Lefschetz公式(0.1)

我们显示第i个周期是RHS(0.4)的一部分。例如，我们得到

(1.8)

通过推进通过。对这个等式的一个非常简单的解释是，定义和(在k群中，通过回拉)的阻碍束的差异可以用的像上的束结构和的回拉束来表示。为了实现这种解释并给出实际的证明，我们在第5节中对空间和束进行按摩-变形，膨胀和扭曲等，以便我们可以得到一个整洁的形式(1.8)。一旦我们对所有i做了这些，然后使用[32，定理1.1]

分解式(1.7)与式(1.6)一起证明定理2。

目录

摘要 1 介绍 2 quasimaps稳定, p-田地和计划 3.的局部定义方程 p场空间 4 完美的阻碍理论 网和虚拟循环 5 约化虚循环的量子Lefschetz性质 6 下属co 来自休息周期的贡献 数据可用性 笔记 参考文献 致谢 作者信息 搜索 导航 #####

3.的局部定义方程p场空间

对于光滑Artin堆栈M上向量束的态射，我们考虑d的核作为一个空间

由同义节表示，有一个切割模型

(2.1)

因此，该回拉复合体定义了一个相对于M的双重完美阻碍理论。

本节的目的是编写(的开放子堆栈)over。

3.1 切割模型的p场空间

不像考虑p域空间没有正则遗忘态射。但是它在本地的定义如下。对于一个点，在C的任何分量上都不等于零，所以我们可以选择一个组合，它的零定义了C上的一个除数并且不与特殊点相交。因为它是开放条件，所以我们有态射

在当地社区。

设为通用曲线上的通用除数，并考虑复数

(2.2)

在[31,Section 3]中解释了我们可以选择它的代表，使得定义在的稳定性条件(1.2)提升到a的总空间，因此这个提升的稳定性条件定义了a的开子堆，那么限制在这个开子堆上的切出模型(2.1)给出了相对于的局部切出模型。

由于我们在本地工作，我们可以假设A和B是平凡的包。那么d可以看作是一个多值函数

(2.3)

定义为它的零的(开放子堆栈)。在本节的其余部分中，我们将通过坐标变化和放大找到d的简单表达式。

3.2 关键的引理

现在我们关注整个部分。我们在当地进行了一些工作，有时没有提及。例如，通过的元素，我们指的是的一个可变局部函数。

正如我们在引言中所解释的那样，考虑稳定的准映射比考虑稳定映射在使量子Lefschetz公式不那么复杂方面有很大的优势。但是(本质上)只有一件技术上的事情需要检查，这在稳定映射中是很明显的——在稳定映射的域曲线附近，线性等价于不相交的光纤1次除数。不幸的是，它不能立即在稳定拟映射的域曲线附近被看到。由于这是在[26,27]中寻找稳定映射模空间的局部切割模型的重要起点，我们需要以下引理。

事实上，这个引理是非常普遍的——它适用于任何不稳定曲线，包括一个2属的稳定拟映射的定义域曲线。设为通用曲线上的有效除数。

引理2.1

局部线性等价于每根纤维上的1次不相交因子的和。

证明的关键思想是通过选择两个线性独立的部分来构造一个覆盖图，这两个部分是模糊的，没有公共零。那么一般点的逆像是d个不同的点。

证明

在最小属2子曲线上选取任意一个局部除数，每个纤维的度数为1且不相交。因为，求值态射是满射，其中表示投影态射。这引出了一个精确的序列

(2.4)

同时，如[27,Section 2.3]中所述，我们可以选择其他除数，并且位于最小属2子曲线上，这样

• ，，彼此不相交，和

• 如果2属分量由两个1属分量组成，则位于不同的分量上。

这样选取除数可以保证。这是一个d阶向量束，因此局部是。通过[27，式(2.5)]，我们得到一个序列

(2.5)

因为，我们可以选择一个映射到0 by的非零局部截面。然后它通过因子，因此，通过(2.4)，它可以被认为是一个部分

也就是0。的正则截面不会消失，并且s在每个光纤上都是线性无关的。

s和的公共零具有纤维度(在每个纤维上可能不是恒定的)，因为s是零，但不是。然后在一根纤维的截面上，定义一个度的形态。因为它不能是1度(这意味着它是同构的)，我们实际上有。普通纤维由不同的除数组成，…，远离，因此我们有

请注意，由此定义的自同构不仅在光纤上，而且在局部上也是同构的。

如果，我们用同样的方法替换，直到得到。然后我们证明了除非引理。现在我们假设。执行度为3的相同过程，该过程从此终止。这样证明就完成了。

考虑上的全称曲线上的全称除数，我们从引理2.1的证明中的精确数列(2.4)、(2.5)得到如下直接推论。

推论2.2

在的局部邻域的派生范畴中，我们得到了由式(2.4)导出的同构。

序列(2.5)诱导同构

此外，[27，引理2.4.1]的类似思想允许我们有更多的同构。

引理2.3

正则单态引出了一个同构

结合所有这些引理2.1，推论2.2和引理2.3，我们观察到它是拟同构的

(2.6)

3.3 Diago带领地方代表的任命

选取任意一个局部恒等式，在(2.6)中可以写成矩阵，。

本节的目标是将矩阵转换成一个漂亮的对角形式

通过使用行和列操作在一个稳定的拟映射的域曲线附近。事实上，Hu-Li-Niu [27, Section 5]已经在稳定地图的区域曲线上进行了研究:在一个固定区域曲线的邻域上，他们发现了一个对角线形式。它取决于域曲线所在的边界分量的类型。由于稳定准地图的域曲线比稳定准地图的域曲线更简单，所以胡丽牛已经给了我们的目标一个答案。下面我们列出了稳定拟映象的定义域曲线。

(1)在一般图像的域曲线附近可以找到一个对角矩阵c

式中节点平滑函数。结合中区域曲线上不存在有理尾的事实，证明来自[27,Section 5.3, Case 1]。在这种情况下，[27]的矩阵包含了配给尾的节点平滑函数和由于其存在而产生的必要的放大信息。它被化简成我们的矩阵。

(2)在图像中的一个域曲线附近可以发现它是

和为中的节点平滑函数。证据见[27，第5.5节，案例1]。注意(1)中的对角线形式由。

(3)在图像的域曲线附近，我们需要放大以获得的对角变换。在我们在下一节讨论它之前，我们先介绍一些我们将使用的有用事实。

当曲线不与(1)的像相交时，矩阵中的条目是根据[27，命题2.5.1]的非消失函数。因此矩阵可以变换成

在哪里

。计算co/核的秩，我们观察到是节点平滑函数和的线性组合。此外，根据[27，第5.4节，情形1]和[27，引理2.7.3(3)]，我们可以假设前两个行列式可以写成

与。因此矩阵被变换成

(2.7)

(13)。当曲线与(1)的图像相交时，[27,Section 5.4, Case 2]和[27，引理2.7.3(3)]表示矩阵变换为

(2.8)

其中为组件(1)的节点平滑函数。

(4)在约简空间的一般域曲线附近，可以发现它是

证据见[27，第5.2节，案例2]。这个对角线形式是通过让(1)

3.4 英航se变化

考虑一下放大的空间

上，矩阵(2.7)和式(2.8)可以变换为对角形式。

在与(1)中的分量相交之外，边界分量是局部的。因此在例外除数的邻域上，我们知道非此即彼。在不失一般性的前提下，我们可以假设。则矩阵(2.7)可以变换为

因此，在放大式中，2.3节中情形(3)的矩阵c的形式为，。此外，(4)中的对角线形式由这个by恢复。

同样地，在与(1)中的分量的交点上，(2.8)变换为

注意(1)中的对角线形式是由这个by恢复的。

全局遗忘态射定义了基的变化。然后将完全阻塞理论和共切的回调定义为共切局部虚循环

通过[19，定理5.0.1]，我们得到了b在(内禀)正锥之间的基变换态射，其阶为1。在[31，定理1.1]中，解释了共截面局域Gysin映射是一种双变算子，因此它们可以通过适当的前推进行交换。这两个证明

3.5 的局部切割模型

回想一下，我们得到了的显式代表(2.6)，其对角矩阵c在第2.3节和第2.4节中作为其微分态射。我们再次强调不一定是全称除数，参见引理2.1。因此，我们应用这些对角化来得到一个局部切割模型，不仅是p场空间的，而且是p场空间的，相对于2.1节所讨论的。推导出的局部定义式(2.3)为

(2.9)

在这里，态射和上面的态射分别代表复合体和，它们的直接和是局部完全阻碍理论(2.2)。在某一点上，第一个态射的核(它是线性的)

参数节，。因此和z一起，它参数化了。第二个态射的核心

参数p域，。

4 完美的阻碍理论网和虚拟循环

4.1 完全阻碍理论

尽管cut-out模型(2.9)在计算方面很有用，但也有两个关键的缺点。一个是它不是全局的，另一个是它没有给出一个裁剪模型，因为它不是平滑的。对于以后的使用，重要的是我们如何将cut-out模型(2.9)的计算应用于或上的完美阻塞理论。在本节中，我们对此进行解释。

首先我们回顾一下完美阻碍理论。我们一直用通用曲线的回拉来表示。局部完全阻碍理论相对于是

这只是(2.2)的对偶的回调。相对而言，全球都配备了完美的阻碍理论

这是通用曲线上的通用线束。和合成的圆锥体

定义了相对于的全局完全阻碍理论。这里表示余切复合体。然后我们有了下面的三角形图

特别是中间的水平三角形告诉我们，局部切割模型(2.9)定义以及自定义是光滑的。脚注3

因此，从局部到全局的一种方法是考虑这种遗忘态射。通过完全阻碍理论的态射

计算可以从一个移动到另一个，前者是全局的，而后者是局部的。例如，平滑度表明两个内禀法锥

是否相关，前者通过包栈的态射映射到后者

这实际上是一个仿射束，也就是说，态射符合束堆叠的确切顺序。确切的证明在[29，命题3]中，但由于它的流畅性，它或多或少是明显的。然后，使用cut-out模型(2.9)对LHS上的锥体进行局部计算，将得到RHS上的锥体计算。

一个解决方案是考虑遗忘态射。因为它也是光滑的，所以是完全阻塞理论的态射

导出了两个本征法锥的关系

也就是说，前者通过包栈的态射映射到后者

像以前一样。它也是一个仿射束，所以结束了。

4.2 虚拟的周期

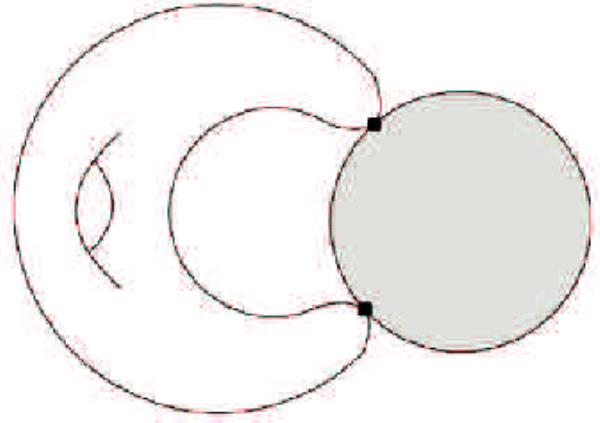
正如在第1节中简要解释的那样，空间被分解为四个不可约的部分

(3.1)

参考引言部分的图片。从局部切割模型(2.9)相对over来看，的<s:1>局部邻域是环的光谱

哪里是一个顺利的邻里。由此我们可以将分解式(3.1)读作如下:

(1)在第2.3节中，我们已经看到了一个点。因此存在图像的一个邻域，其逆具有不可约分量

考虑一个观点。由于点是一个2:1的图像，我们考虑一个可变的邻域。在这种情况下，存在一个其逆像为

注意，这并不意味着它是可简化的。上面的描述是关于 邻里关系。注意，不满足。所以邻里可以选择不见面。

接近一个点，我们有。所以存在一个邻域它的逆像有

(13)在某一点附近，可被两个节点平滑函数整除，如和。存在一个邻域，其逆像有

在外面的一个点附近，我们有。因此存在一个邻域，在其上定义。

然后将内禀法向锥分解为

(3.2)

前四项中的每一项都被定义为补开部分的闭包。例如,

它们实际上是闭包，因为它是一个封闭子堆栈。事实上，我们可以从cut-out模型(2.9)中检查(3.2)中的“others”是空的，这样我们就得到了一个分解

(3.3)

这里有一个简短的解释。让我们从它的光谱中读出分解，一个回调

(3.4)

我们知道在(3.4)中没有高阶关系。在远离交点的地方，锥是每个不可约分量的一个束。所以所有的关系都是线性的。由于Spec(3.4)是包含在圆锥体中的闭包的并集，因此在交点上也不应该存在高阶关系。

(1)在(，)点附近，分解为不可约分量

我们可以用下面的方法来检验不可约性。我们观察到，是束上光滑变化自杀的关系。准确地说，它是

(3.5)

因此它是不可约的。另一方面，我们观察到的是光谱

这是一种光滑品种的纤维，其纤维是空间中一点膨胀的仿射锥体。因此它也是不可约的。在其他情况下，我们可以用类似的方法来证明分量的不可约性。

不可约性保证了它们分别是和的基本变化。注意，over，是一个包，因为是自由变量，应该成正比。

(2)在一个点附近，分解成

这些分别是和的基数变化量。除以，是一个2阶的束。

(3)在(，)点附近，分解为

它们分别是和的碱基变化量。结束，是一个捆绑包。

(13)在一个点附近，可以被整除。在本例中，被分解为

两者都是捆起来的。

(4)在(，)点附近，是一个束。

所以我们可以检查是否有' others '。将其与的(局部)等价结合

3.1节中讨论的给出了分解(3.3)。

注意，切出模型(2.9)告诉我们态射(通过组合定义商)取的值

(3.6)

因为，，和。例如，我们有这意味着。

在[6]中引入的定义(1.5)中提到的局部虚循环的共截面确实是在上面的阻塞轴上定义的。这就给出了派生范畴中的态射。文献[6]证明了这实际上是通过绝对双重完全阻碍理论来实现的。因此组合定义了束堆栈上的共截面局部Gysin映射[28]。

对于下面的定义，我们使用完全阻碍理论

。然后，上述回调在bundle堆栈上定义了cosection本地化Gysin映射。我们把这个应用到分解3.3。

定义3.1

简化部分的虚循环

由共截面局域化Gysin地图的图像定义。循环和类似地分别通过使用和来定义。

因此，我们得到虚类的分解

通过下推提供(1.7)。

5 约化虚循环的量子Lefschetz性质

考虑定理1和定理2中的束，它被精确定义为

万能曲线上的万能线束在哪里?与第2.5节一样，通过局部替换，我们可以使用局部截断模型(2.9)来检查V是局部自由的，参见[27，命题2.1.3]。注意，这并不意味着

是本地免费的。通过态射每个点都有一个section数据。然后，定义X的方程，取通用截面u到。它定义了定理1和定理2的细化欧拉类。

在证明以下命题之前，请注意，我们几乎可以用与[33，命题4.1]，[34，章节4.3]相同的方式来证明它。但在这里，我们将给出另一个证明。

注意和，这是平滑的。

命题4.1

约化后的虚循环满足原量子Lefschetz公式(0.1)

证明

考虑来自cut-out模型(2.9)的诱导完全阻塞理论，以及它对(是的开放密集子集)的限制。它引出了一个地方代表，也就是

(4.1)

第3.2，(3.5)节中的圆锥体分解说明

(4.2)

另一方面，我们有以下态射:

这里，第一个箭头是从束堆栈到它的粗模空间的态射，粗模空间也是一个堆栈。第二个箭头来自分解

对于投影，它来自[32，(3.15)]。第三个箭头是规范态射。

(4.1)的地方代表说，这篇作文是附形的。而且，(4.2)说它的核局部表示为在F中，因此它等于。

因此，通过使用共截面局域化Gysin映射的函子性质[36，定理1.4]，我们有

注意组成

是给定的余割。因此等于

6 下属co来自休息周期的贡献

6.1 有限公司梗阻束内

在本节中，我们考虑我们的空间，因此使用完全阻塞理论，分解(3.3)和定义3.1的虚循环。让

作为具有遗忘映射的切割模型(2.9)的局部光滑空间，对偶完全阻碍理论是局部同构的

我们使用这个局部表达式来检查

是本地免费的。我们表示它的对偶。注意，这不是

在交叉路口不是局部免费的。在交集之外，它们是同构的。这里的阻塞束也是如此。从束到阻塞束存在诱导态射，这是交集外的同构，但它甚至不是交集上的注入。

选取任意的全局局部自由代表，我们得到一个图

用这个我们定义为回拉的图像。然后利用函子性质[36，定理1.4]求出循环

是根据定义3.1。我们用脚注5表示这张kim - li的共截面局域化Gysin地图，这样我们就可以写

(5.1)

现在我们考虑其他的内禀法锥

结束了。由于在其图像上光滑，我们得到了完美的正切复合体

，哪里是图像

1. （1)

   ，

2. (2）

   ，

3. （3）

   ，

在节点识别态射下。在这里,

表示在和时定义为交点的除数。我们需要扭转因为局部限制的法向束不同于交点除数限制的法向束。然后是锥体

是否与bundle堆栈同构

。我们定义它的回调

然后组合定义态射

(5.2)

使用(3.6)，我们看到第一个箭头是局部的

1. （1)

   ，

2. (2）

   ，

3. （3）

   ．

因为消去了定义方程，比如

态射因子通过

在与其他组件的交集之外，映射同构于。在交叉点上，它映射为零，在任何一个或消失。因为它是一个包，我们可以期望使用它而不是用于计算(5.1)的优势。这不是一个荒谬的幻想，因为它们在交集之外是同构的。

例5.1

局部结构环(3.4)告诉我们，(局部)是的谱

所以是一个线束，但有完整的秩。同时根据它的定义

是(局部)的谱，其中变量Y是的坐标。因此是一个线束。态射是

它同构映射到，但是映射到0。

在膨胀的B和齐次坐标函数上，我们考虑锥

向下推到向下的形态。回拉锥体映射到这个锥体，它在例外轨迹之外是同构的。由于它是线束之间的态射，因此锥被例外除数扭曲是同构的。因此，我们可以使用它的下推而不是(5.1)。

6.2 定理2的证明大纲

let，(2.9)给出了的局部裁剪模型。对其进行分解(3.1)，得到对应的(3.1)

然后，组件是以下节点识别态射的映像

1. （1)

   ，

2. (2）

   ，

3. （3）

   ．

式(1)中，为along的放大，定义为。爆破轨迹是爆破前(1)与(3)交点的一部分。(3),

表示对偶同义线束和的投影。下面的注释解释了为什么是图像。

话5.2

其实，应该是(形象的)投影的回调

On since是放大后的底变化量。它等于

如果打开。注意，评价图诱导了从霍奇到同义线束的态射。在[43,pp.1221-1222]中，Zinger证明了它同构映射到

式中为两个标记点碰撞的边界除数。因此我们有

正如我们在第1节中提到的，用(2.9)的局部计算告诉我们，第i个p场空间是一个矢量束，

为了避免混淆，我们将其表示为当我们将其视为一个束或局部自由束的局部部分，但用于空间。所以on的回退是同义反复的捆绑。在第5.1节中定义了梗阻束。由[32，式(3.15)]证明，分解为:

从现在开始，为了简单起见，我们用态射的定义域、纤维积和的回拉来表示。明确地,

1. （1)

   ，

2. (2）

   ，

3. （3）

   ，

这个bundle是

1. （1)

   ，

2. (2）

   ，

3. （3）

   ．

回想一下，在(3)中，两个评估映射是相同的。我们用

节点识别态射的碱基变化。让。然后分解为

1. （1)

   ， ，

2. (2）

   ， ，

3. （3）

   ， .

然后将回拉截面分解为

对偶完全阻塞理论(1.4)的共截面分解为p.(df/dx)。

和f，它们分别对应于和。

利用这些共切面，我们可以定义Kiem-Li的共切面局域化Gysin地图

和。令[36，定理1.4]的乘法性质告诉我们(5.1)变成

(5.3)

从第二节开始

由第4节中定义方程f在V上的对偶定义，则循环在

式中，f(u)为(1.1)定义的回拉方程。这种支持是同构的

，在哪里?然后是第一共分割的限制

这种支持是由弹射引起的

其核是，如下所示。On, df定义了一个短而精确的包序列

(5.4)

在哪里

1. （1)

   ，

2. (2）

   ，

3. （3）

   ．

的同义剖分定义了的共剖分，复合剖分定义了的共剖分，这是的限制。将乘法性质[36，定理1.4]应用于数列(5.4)，我们有

(5.5)

式中为Fulton-MacPherson交同态，或Gysin映射。

在第5.3节和第5.4节中，我们将分别解释下面的第二个和第三个等式。其余的等式和符号在等式后解释:

(5.6)

第一个等式来自式(5.3)和式(5.5)。我们用(5.2)的回调来表示。既然是一捆，那么越过哪一捆就是光滑的。类比命题4.1，我们可以证明是的回调周期

1. （1)

   ，

2. (2）

   ，

3. （3）

   脚注6

通过。

我们用。表示这个回调周期。这就解释了第四个等式。同样，我们用by表示回拉周期，用by表示回拉周期。

的余割由的同义余割给出。

这样就得到了第五个等式。在第5.4节中，我们将看到包(经过除数扭转后)包含在

。由于不存在p场，构成的同义部分

还有同态

In(5.4)在圆锥上为零。因此圆锥体包含在核中

，它证明了最后一个等式。

在第二个等式的RHS中，我们用

的限制的结束。如果圆锥与乘积同构，则第二个等式成立。

不幸的是它不是乘积，但是我们把它变形成乘积然后用这个变形来证明第二个等式。我们在5.3节中讨论了这一点。

我们知道(5.2)在交集之外是同构的。然后在放大后用除数取扭曲，得到一个包含第三个等式的同构。这项工作在第5.4节中讨论。

得到(5.6)后，我们证明5.5节中的定理2。当X是Calabi-Yau三倍时，我们证明5.6节中的定理1。

6.3 锥体变形

我们从圆锥体开始。交点被定义为由的同义段切割出来的。因此我们有

这个锥体是对法向锥体的通过变形的变形[21，第5章]。如果我们写，它就是

因为和分别独立于P和X，它们在上消失，所以它们在任何一个上都是零。

引理5.3

圆锥的限制是它的分量。此外，它与产品同构

(5.7)

其他成分在被吸收后消失。

证明

我们使用cut-out模型(2.9)得到的3.2节中的局部坐标环来证明这一点。回想一下(3.4)，局部是Spec of

(5.8)

的局部坐标环。

在或中的点的邻域中，我们已经在2.3节和2.4节中看到，因此。通过节点识别态射进行回拉，是由3.2节中描述的定义的组件，定义为

。回想一下，它是由同义反复的部分切割出来的

。引入一个伙伴变量，它构成的基(因此它们是线性函数)，锥是Spec的

那么它就是and的并集。我们用。这样做就足以证明它消失了[36，定理1.4]。我们用程度来说明这一点。这个循环是度的循环

另一方面，则包含在共切点的简并轨迹中。它包含在维数小于或等于Thus的数组中。组件是Spec

它定义了锥(5.7)。

圆锥体定义为，并且是加法。然后它有4个分量

同样地，我们可以显示前三个人将被按程度原因杀死。恰恰是第一个被。该包被分解为两个部分，因为它的双元包是由。我们用每一个杀死第二个和第三个。第四个是圆锥形(5.7分)。

引理5.3表明

它证明了式(5.6)的第二个等式

6.4 锥体的局部自由度

在本节中，我们将向量束联系起来

还有蛋筒。我们在整个部分中抑制符号和，这分别意味着和与局部坐标。

对于，我们考虑沿交点的原像的放大。表示例外除数。

引理5.4

For, bundle会单射映射到。此外，周期向下推至。

证明

考虑式(5.2)的回拉态射及其与第一个和的投影的组合，

(5.9)

它是在交集之外的注入，因为

同构映射到那里，它在本地包含在。通过(3.6)和下面(5.2)的计算，它在相交的原像上消失。因此，扭转的回调映射到。

周期向下推到(5.9)图像的结束处，即。

对于，我们考虑两个放大的组合:首先是沿交原像的放大，然后是沿交原像的固有变换的放大。让,

分别表示第一项和第二项的例外约数。然后分解为

因为的原像的固有变换是对应于节点的两个不同分量的不相交并。我们可以在当地检查第一次爆炸是否被带走了。和的固有变换是不相交的。让和。

回想一下，这个bundle是正常bundle的回拉，

引理5.5

束内映射到，它的基本循环向下推到。

证明

for的态射(5.9)是和之外的注入。它在的原像上的秩为1，在的原像上消失。因此，第一次拉回的扭转量在固有变换上是1级的。因此注入。

随着(5.9)图像的闭合，周期向下推至。

现在我们用引理5.4和5.5来解释式(5.6)的第三个等式。事实上，这些引理表明

因此，由第三个等式可知，(5.6)必然是

同时[34，引理4.1]表明，最后一个方程的分母对下推后的结果没有贡献。这意味着我们得到(5.6)

(5.10)

Where for和for。

6.5 定理2的证明

回想一下，这是放大态射的碱基变化。在本节中，我们使用(5.10)显式计算得到定理2。

6.5.1 情况下

引理5.6

我们有

其中上同调类，和在引言中定义。在最后一项中，是用的标记点来定义的，B是用定理2中描述的点来定义的。

证明

回想一下第5.2节

• ，

• ，

• ．

这里是例外除数，它是在第5.2节开始定义的投影。我们用这些来计算(5.10)。

首先，我们可以计算

然后用态射的投影公式

应用于(5.10)，则RHS中第一项K对的贡献为

由[32，定理1.1]，我们得到

所以贡献就变成了

接下来我们计算第二项的贡献。这一项是循环的推进，

(5.11)

因为正常的束是。

为了计算它对使用投影公式进行嵌入的贡献，我们需要用(5.11

而不是in degree of which是。对于这个投影公式，我们用。

然后我们需要把它推到通过向下的态射b。

注意，下射态射b /是投影态射。然后根据Segre类的定义[21,Chapter 3.1]，我们有

所以用(5.11)封顶并把它推到，投影公式给出

(5.12)

在程度上。那么对的贡献是(5.12)。为了计算它，我们先计算一下

(5.13)

通过嵌入和绑定表示，求值态射产生一个序列

用对角线类表示，(5.13)变成

其中为(0.3)中定义的周期。请注意。因此贡献是

6.5.2 情况下

回想一下第5.2节

• ，

• ，

• ．

把这些代入(5.10)得到下面的引理。

引理5.7

我们有

6.5.3 情况下

引理5.8

我们有

其中上同源类在引言中定义。在最后一项中，是用的标记点来定义的，B是用定理2中描述的点来定义的。

证明

回想一下第5.2节

• ，

• ，

同义线束在哪里

是一个约数。我们用这些来计算(5.10)。类展开为

我们计算第一项对。它扩展到

它的度-部分是

把它盖上，把它压下去，它就变成

(5.14)

对的贡献是(5.14)也就是

现在我们计算第二项的贡献。它是循环的推进，

这里我们使用了一个事实，即正常束与双Hodge束同构，并且束位于点上(因此它的第一个Chern类为零)。这就变成了

延伸到

它的度部分是

把它盖上，把它压下去，它就变成

(5.15)

在程度上。所以对的贡献是(5.15)也就是

然后引理5.6-5.8和(1.6)证明定理2。

6.6 比丘三倍

假设X是卡拉比-丘三倍矩阵。集

6.6.1 情况下

既然我们有

它对积分的非平凡贡献是。另一方面，由于和的(复数)次幂是2，我们有。因此

使用[32，推论1.3]

我们获得

(5.16)

6.6.2 情况下

类似地，我们有

重要的贡献是。因此我们得到

(5.17)

6.6.3 情况下

因为，我们有。

由式(5.16)、式(5.17)、式(1.6)证明定理1。

下载原文档：https://link.springer.com/content/pdf/10.1007/s00208-023-02689-5.pdf